Lecture 1. Introduction and History of ZKP
video: https://www.youtube.com/watch?v=uchjTIlPzFo
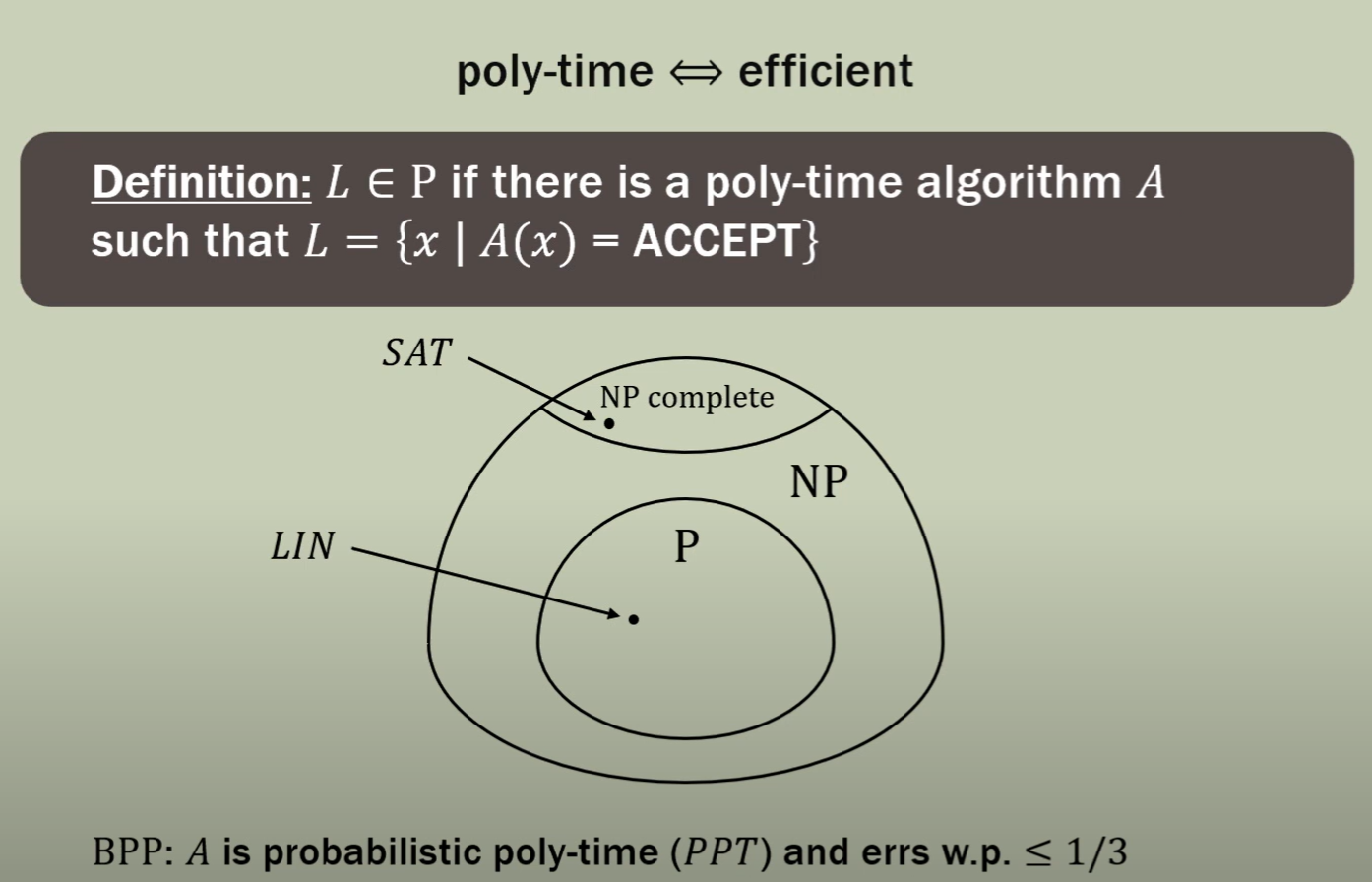
NP-Language:
| Definition: \(\mathcal{L}\) is an NP-language (or NP-decision problem) if there is a $$poly( | x | )\(time verifier\)V$$where: |
Completeness: true claims have short proofs, s.t. if \(x\in \mathcal{L}\) then there is a $$poly( x )\(size witness\)w \in {0,1}^*\(such that\)V(x,w) = 1$$. - Soundness: false theorems have no proofs, s.t. if \(x \notin \mathcal{L}\) then there is no witness, so \(\forall w \in \{0,1\}^*\), we have \(V(x,w) = 0.\)
[critical thinking]
Is there any one-prover-many-verifiers or many-provers-one-verifier or many-provers-many-verifiers?
Proof System
video: https://www.youtube.com/watch?v=6uGimDYZPMw

NP Proof System:

example 1: Boolean Satisfiability:

example 2: Linear Equations:
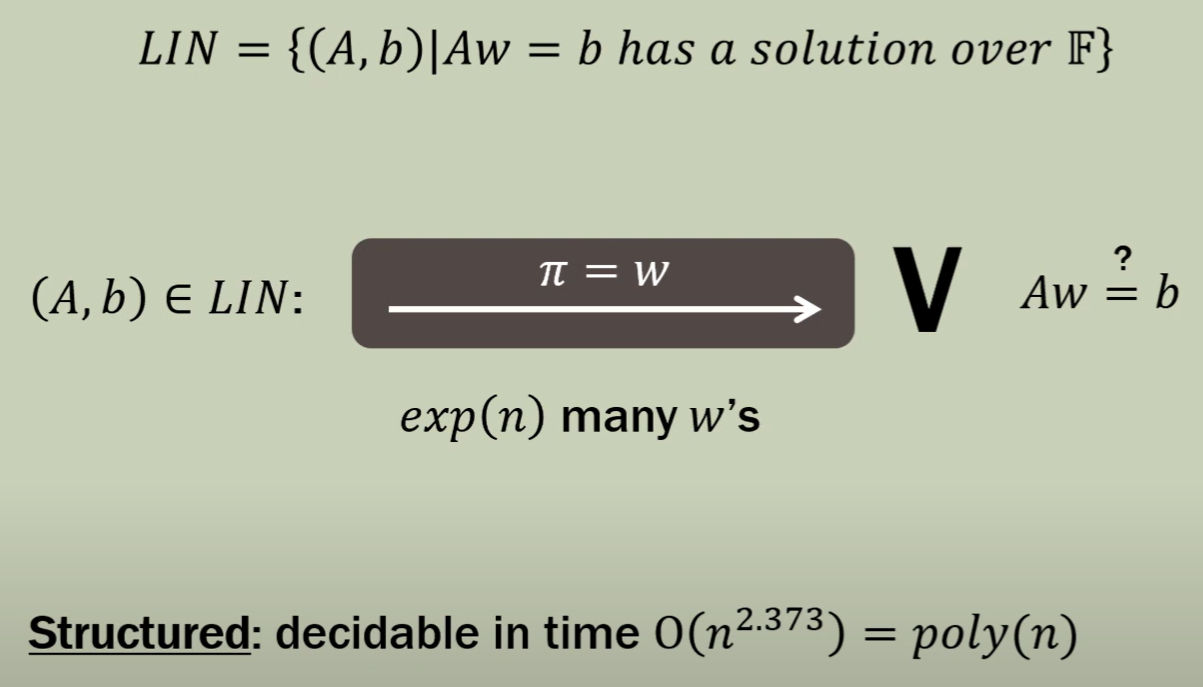
The class P (ploynomial)
example3 : Quadratic Residuosity:
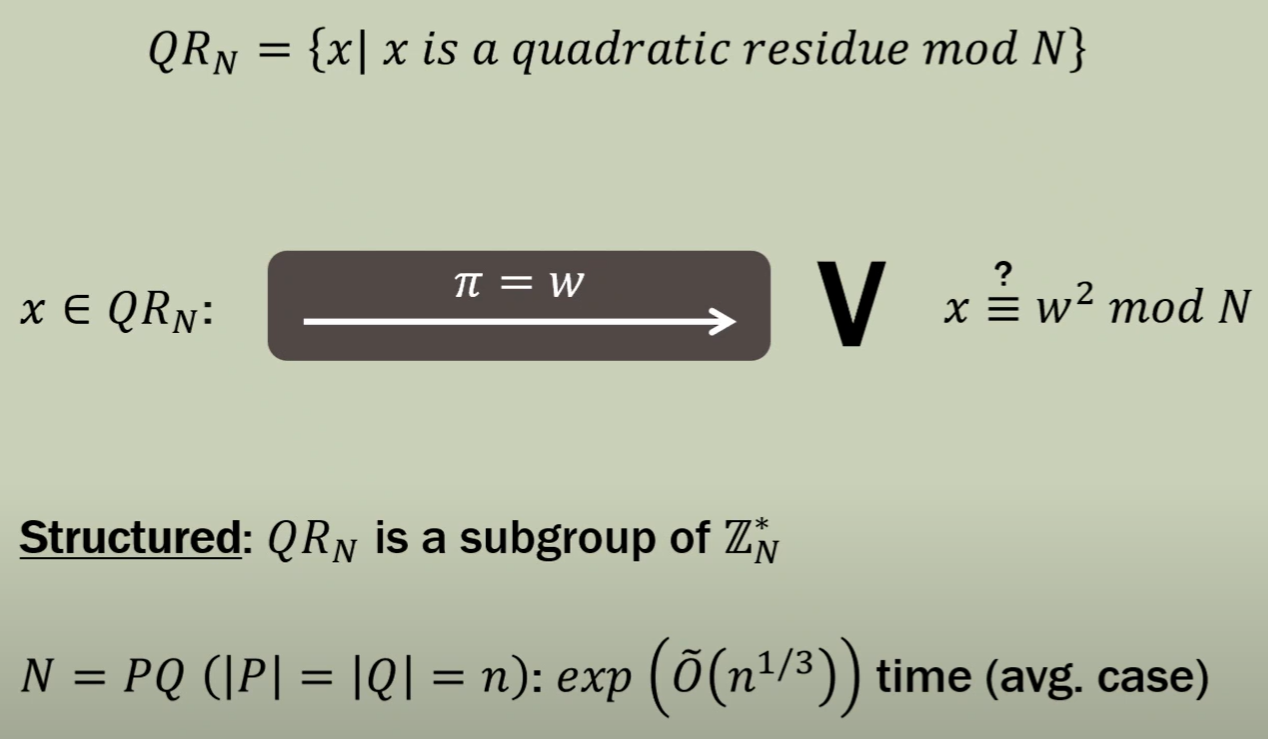
Interactive Proof:


the power of IP:
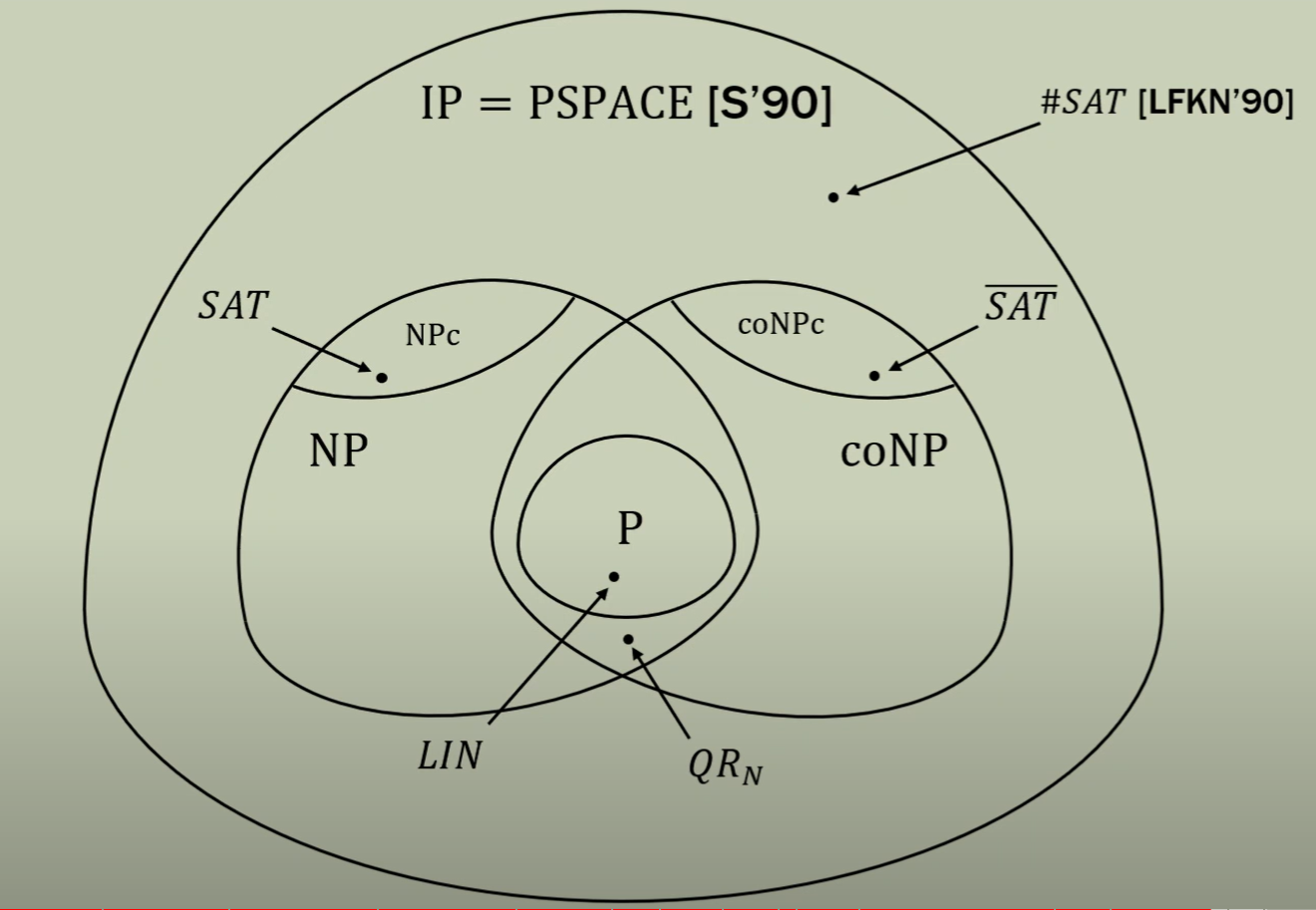
Zero-Knowledge Proof
Definition of “no knowledge leaked”

Definition of “Honest Verifier Zero-Knowledge”

a zero-knowledge proof for QR_N:

Definition of “Perfect Zero-knowledge”
video : https://www.youtube.com/watch?v=cQ-BI1WWzjU

Definition of “Statistical Zero-knowledge”

Definition of “Computational Zero-knowledge”

Commitment Scheme
statistically-binding:

Zero-Knowledge Proofs of Knowledge
Yehuada Lindell
Bar-llan University
video: https://www.youtube.com/watch?v=RvGsjnoYRRg
Lecture 2. Overview of Modern SNARK Constructions
video: https://www.youtube.com/watch?v=bGEXYpt3sj0
SNARK:
succint: “short” and “fast”
zk-SNARK:
succint and reveal nothing
What is SNARK:
arithmetic circuit:

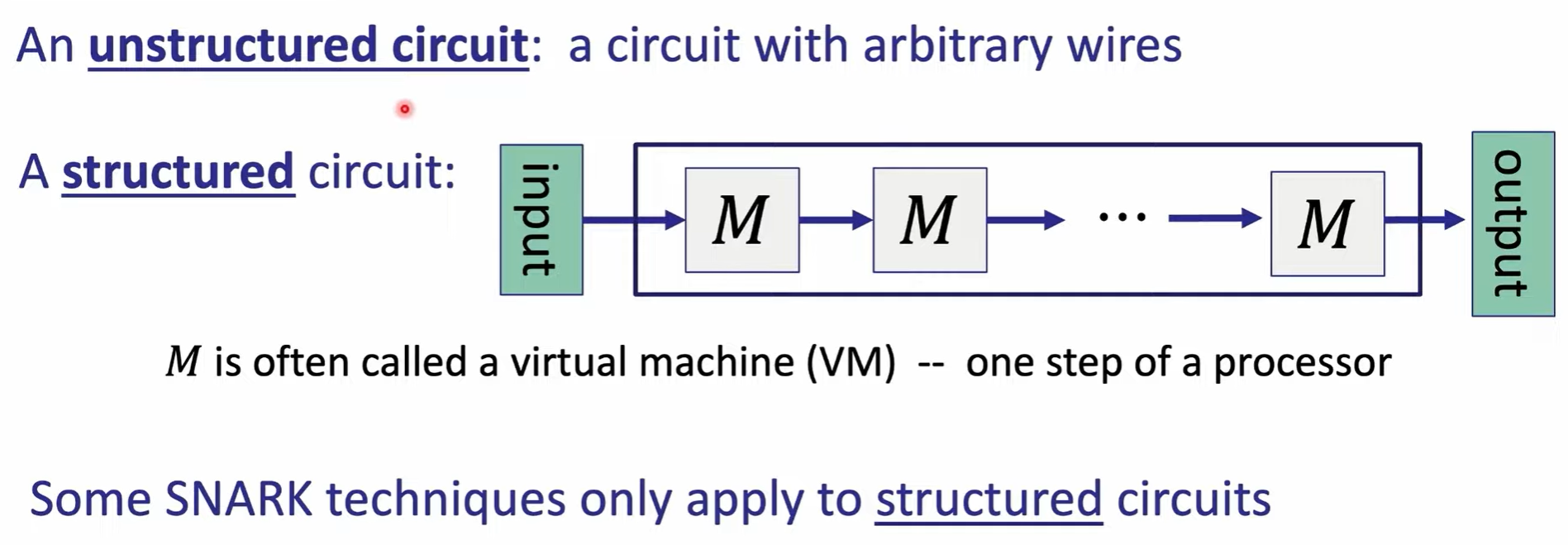
NARK:

SNARK:


Types of Preprocessing Setup

better from top to bottom
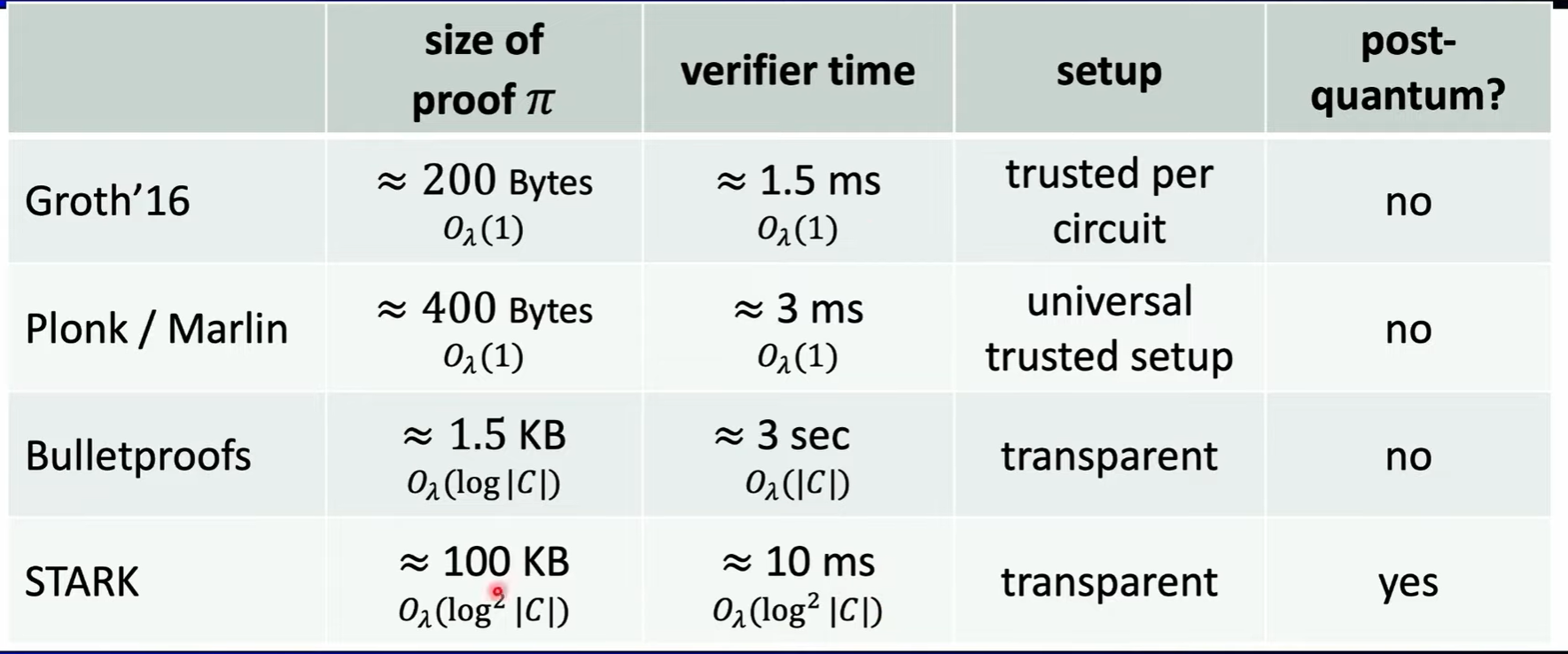
Significant Progress
| (for a circuit with about \(2^{20}\)gates) (prover time is almost linear $$ | C | $$) |
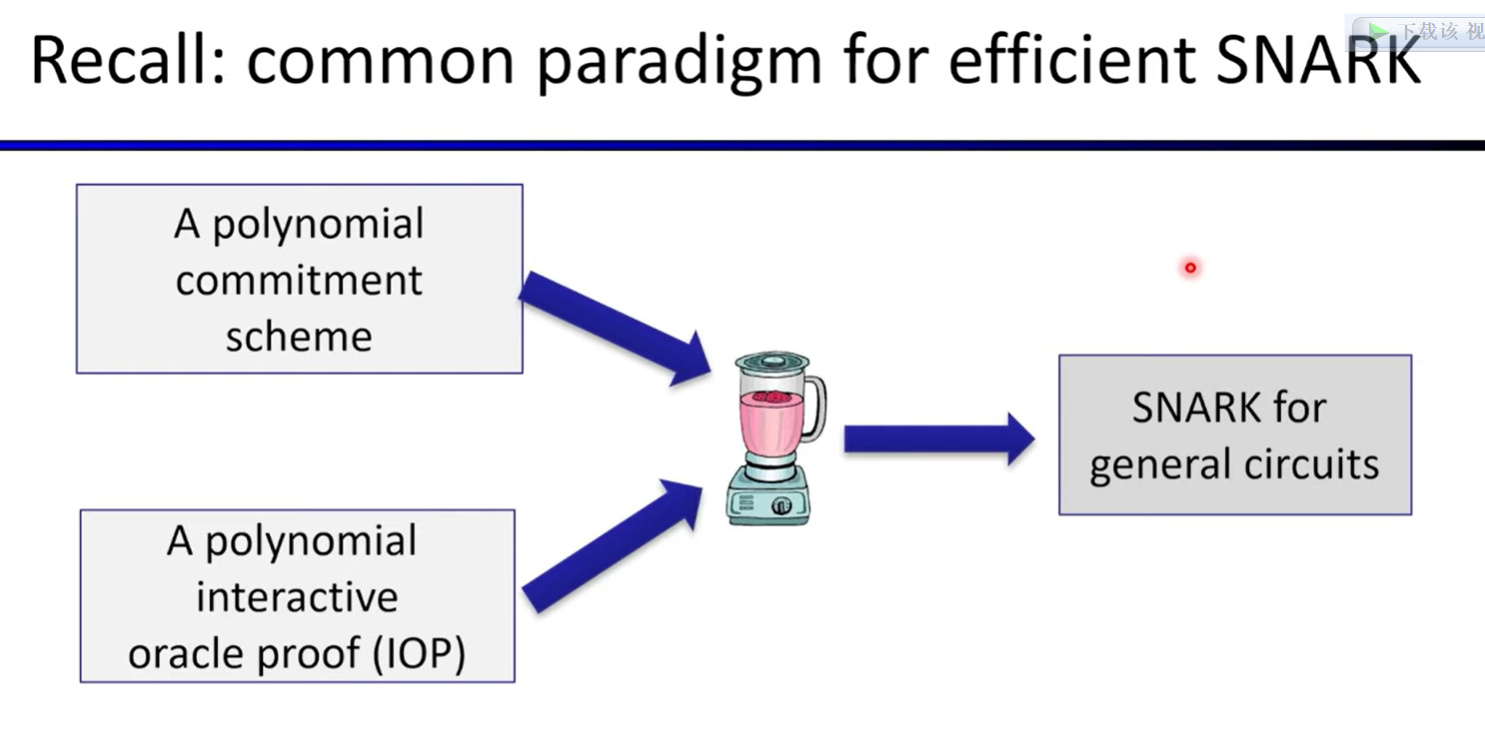
Building an efficient SNARK
Paradigm:
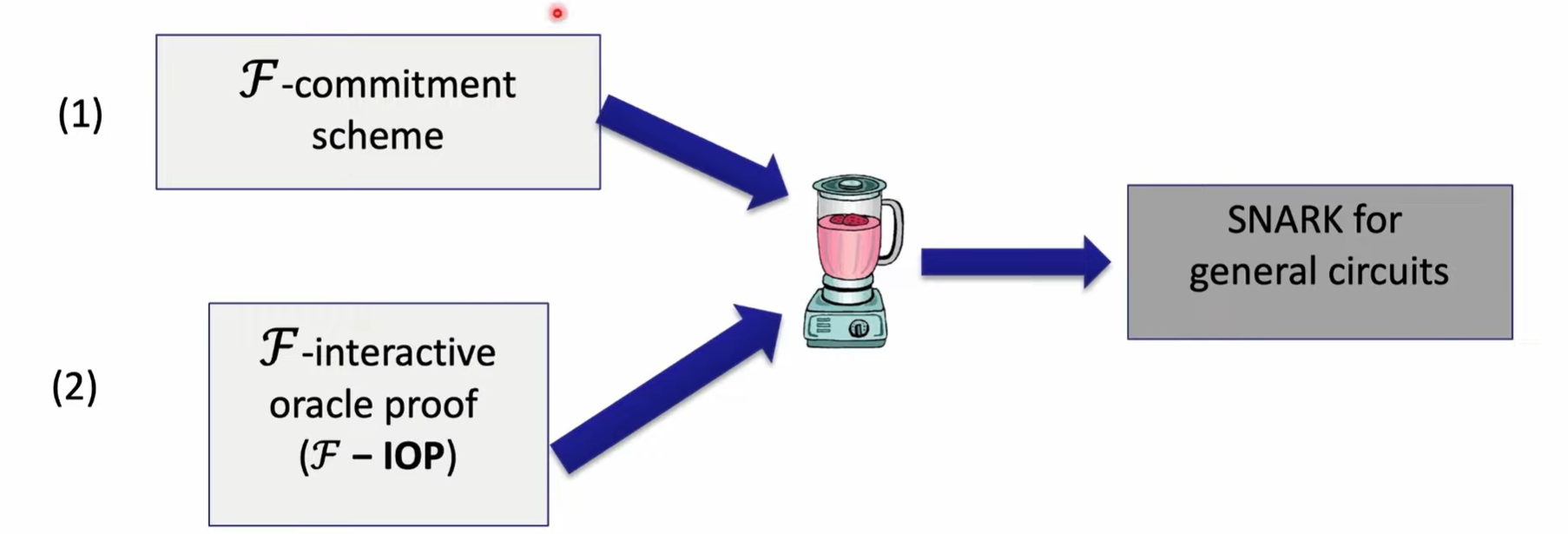
functional commitment:

e.g.

Fiat-Shamir Transform

Functional-IOP:

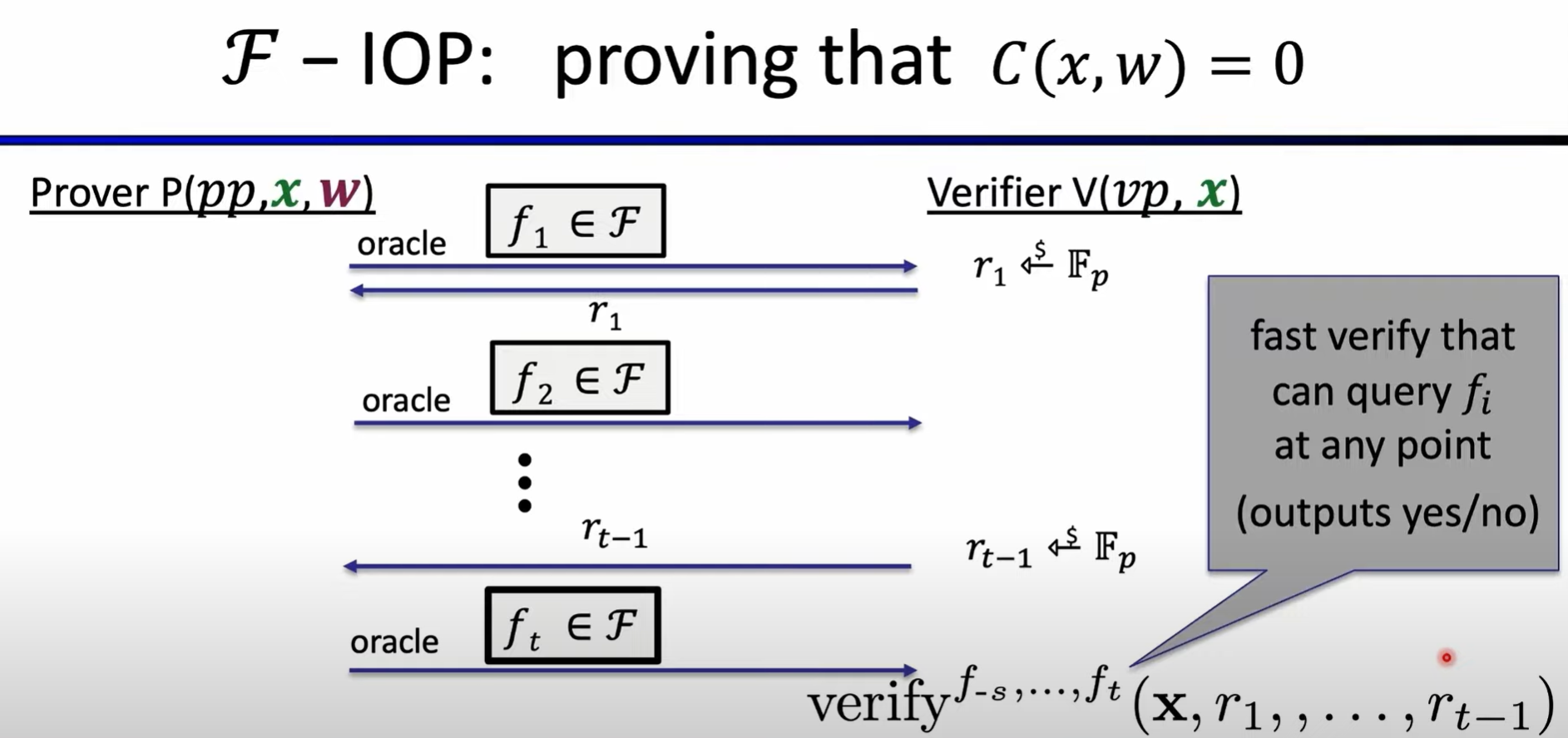
SNARK in Practive
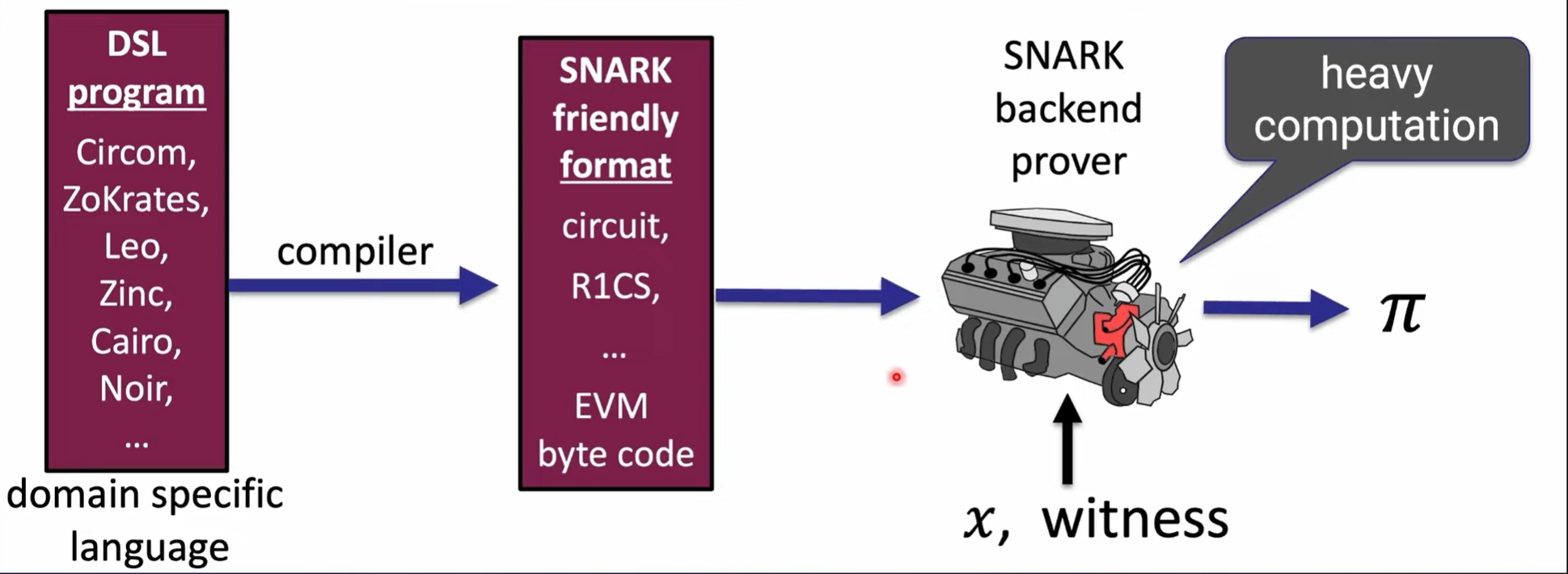
Lecture 3. Programming ZKPs
paradigm:
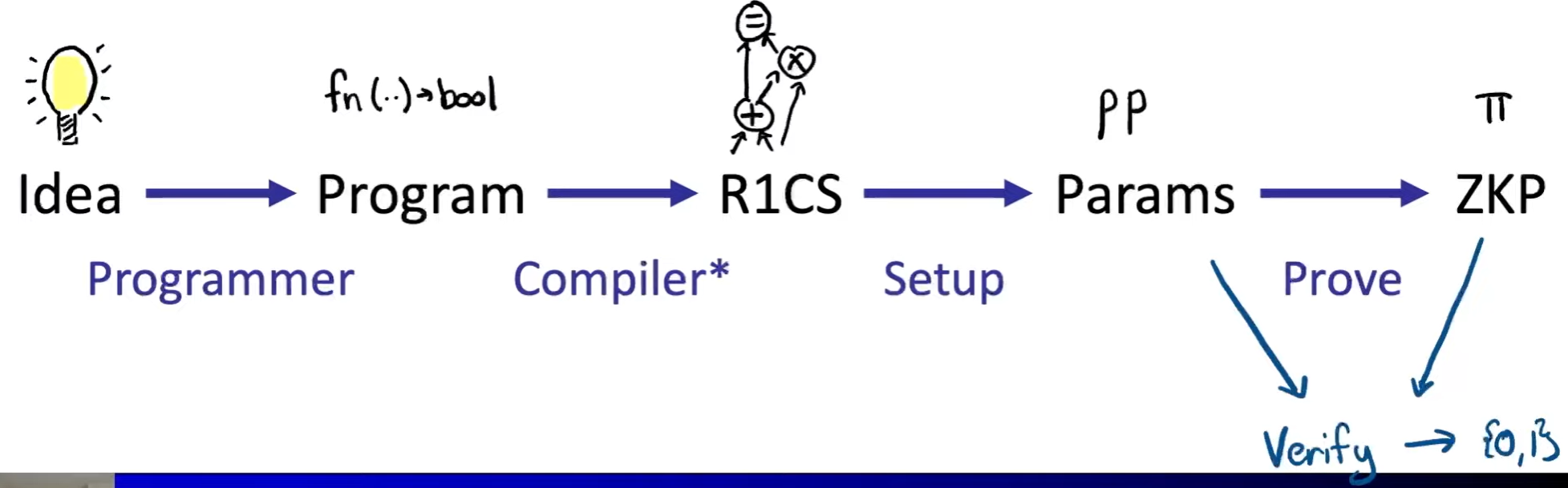
e.g.
ZKP programmability:
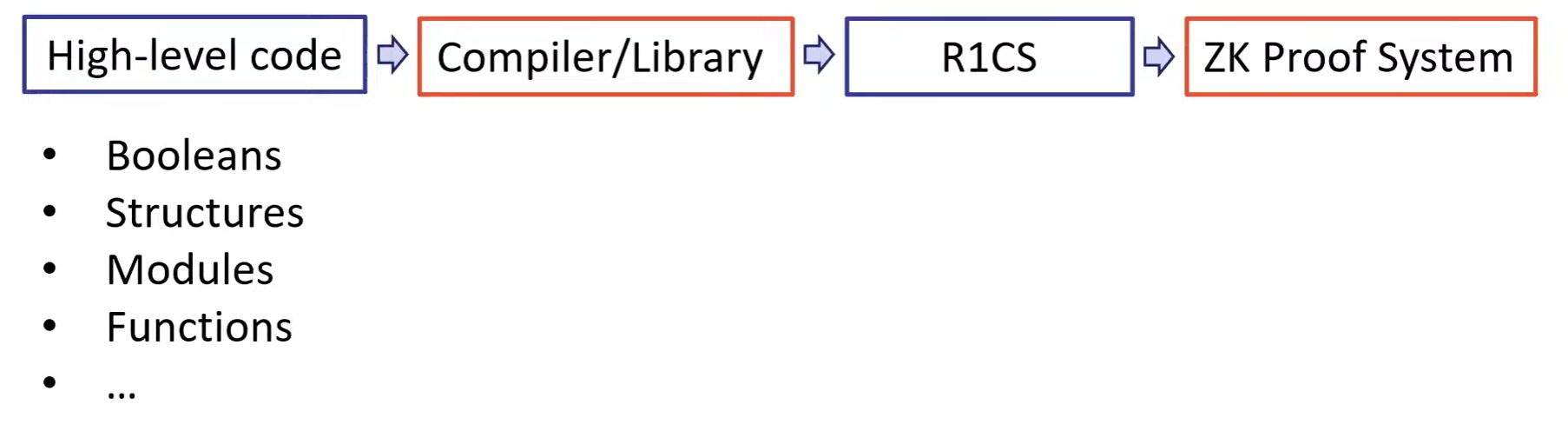
Arithmetic Circuits:


R1CS


write an AC as R1CS:
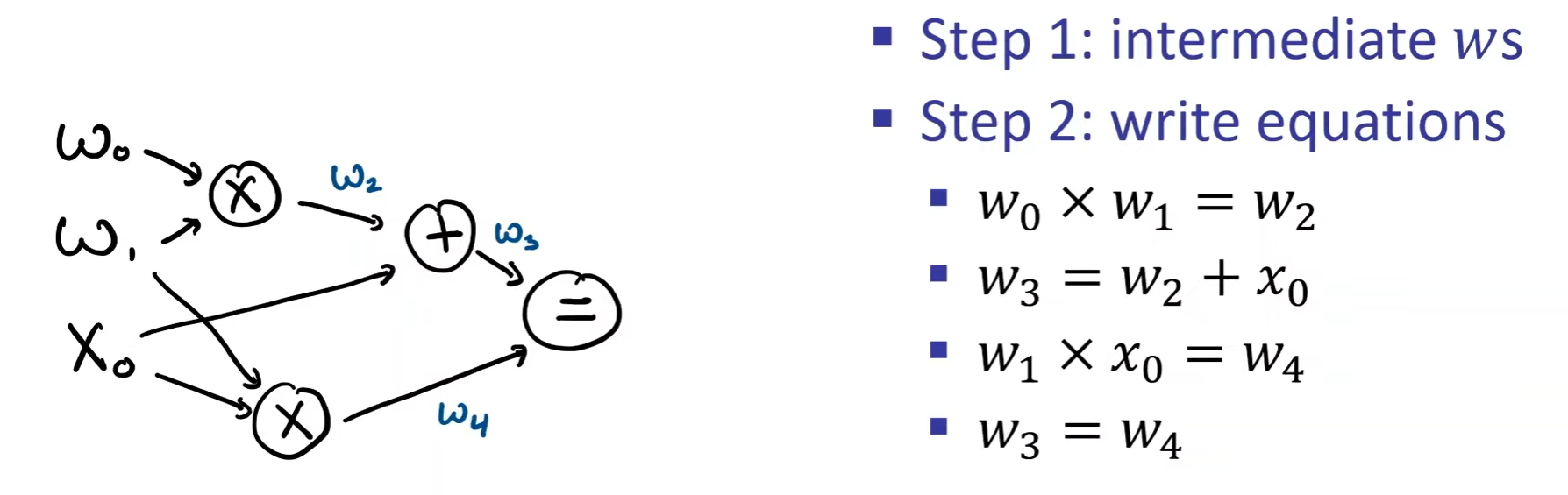
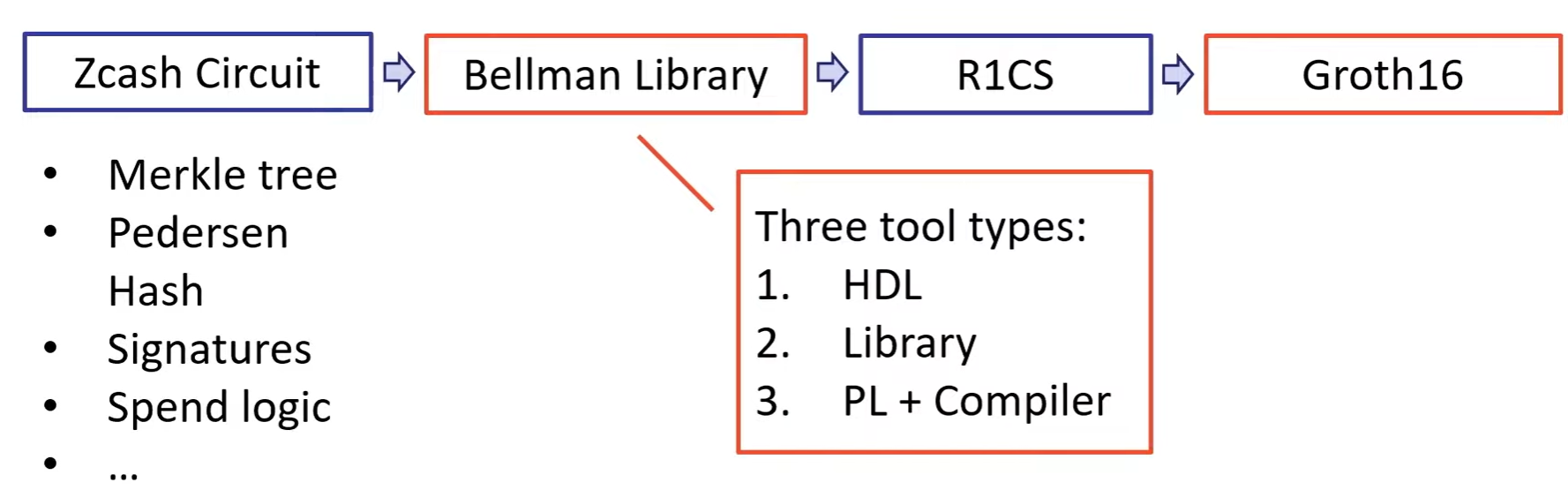
1. HDL: Hardware Description Language

e.g.

Circom:
base language:



2. A Library for R1CS:
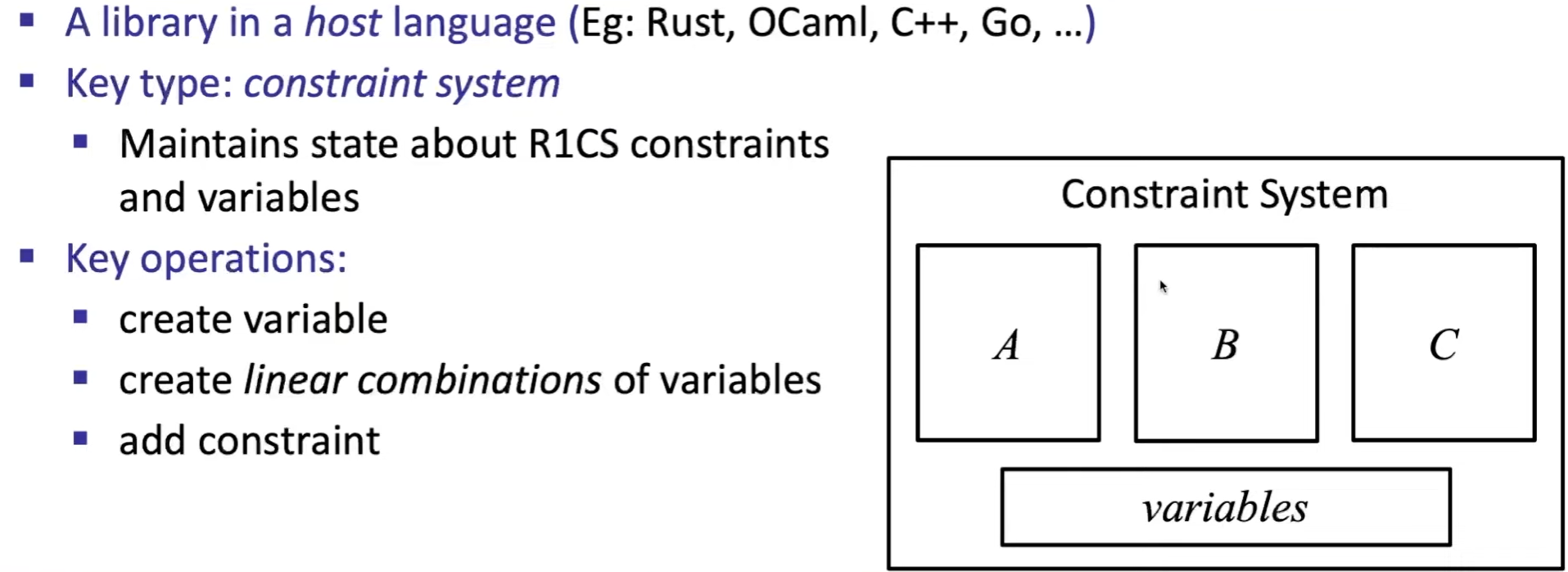
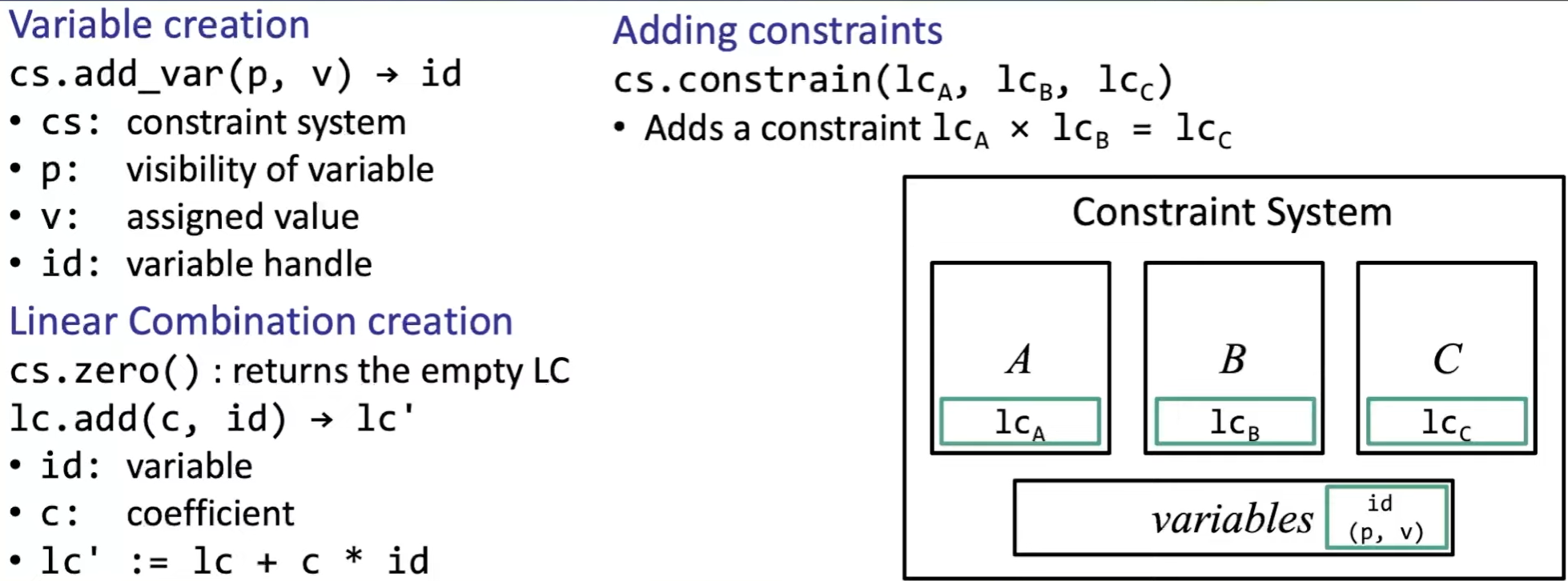



witness computation:

3. High Programming Language:
Zokrages:


witness computation:

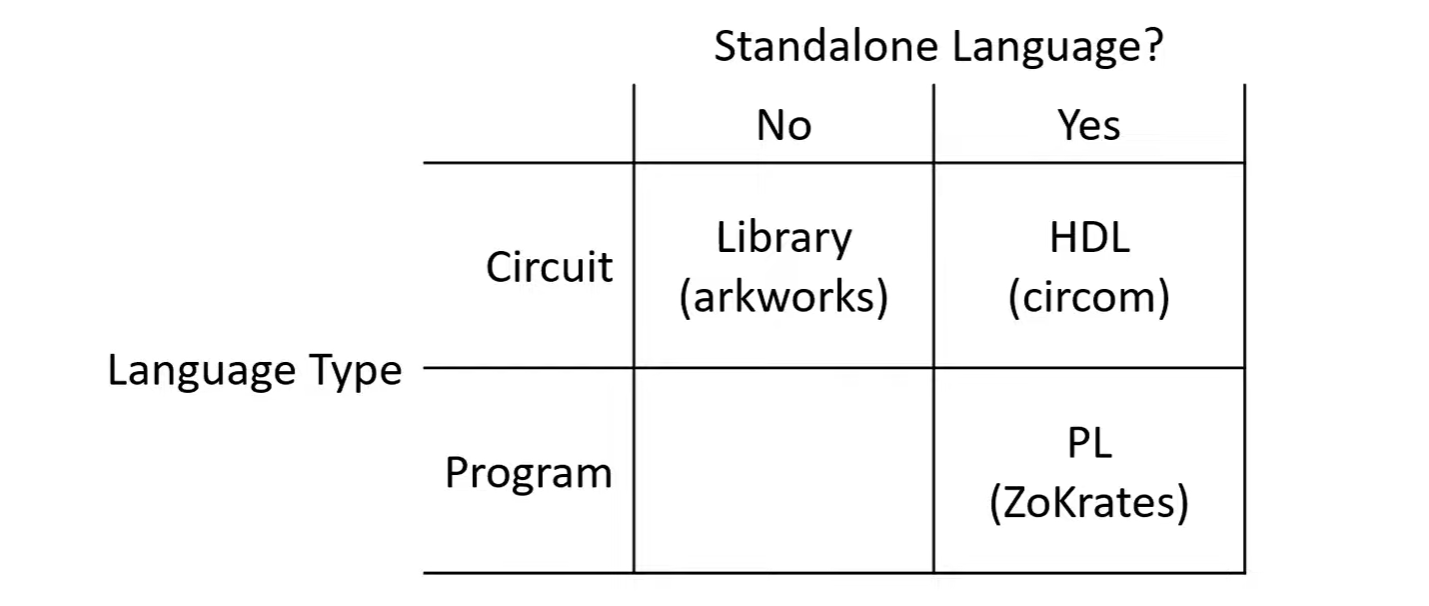
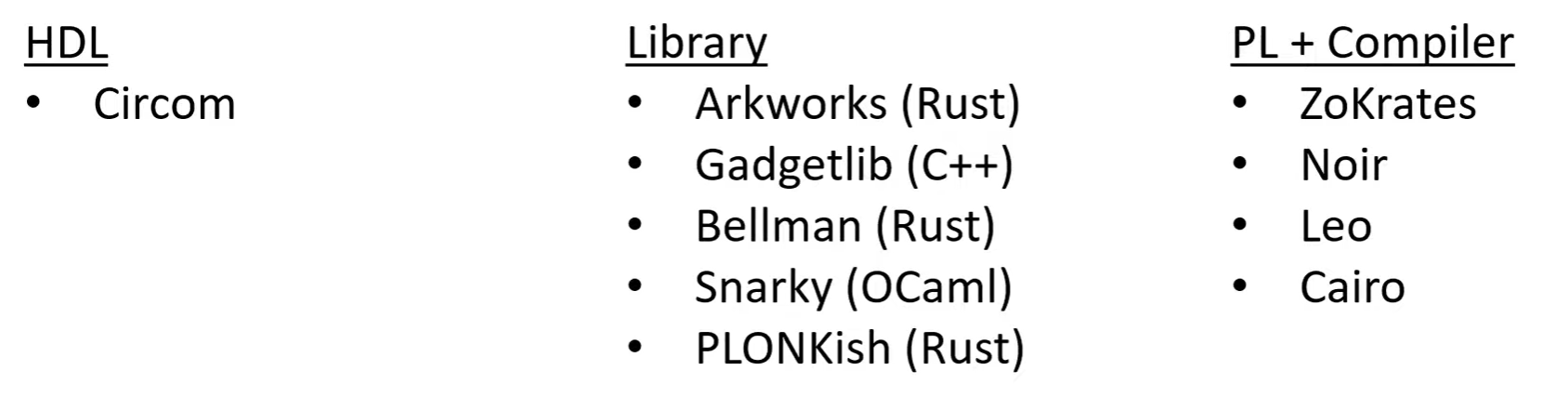
ZKP Toolchain
Toolchain types:



Lecture 4. Interactive Proof.
Definition of IP

soundness vs knowledge soundness:

IP Design
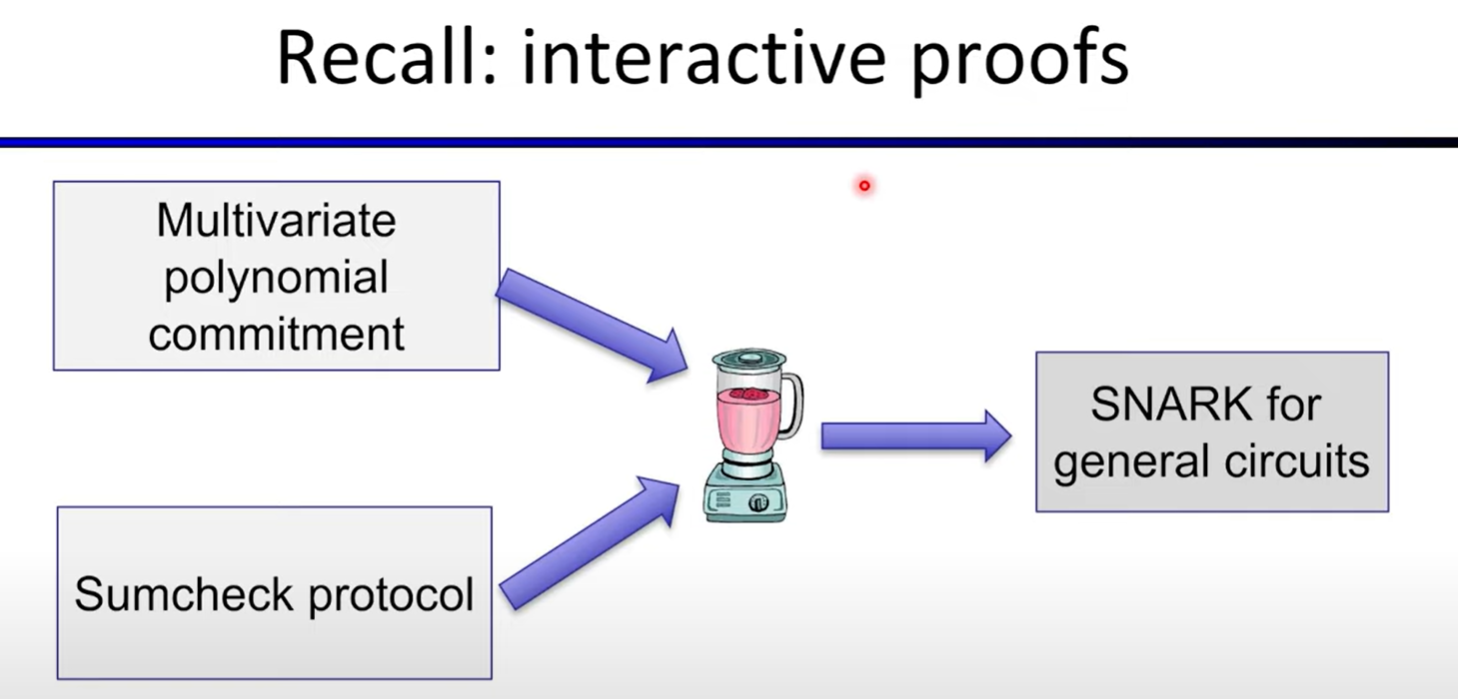
The sum-check protocol


An application: Counting Triangles:

Polynomial IOP:

rewinding technique to proof knowledge soundness
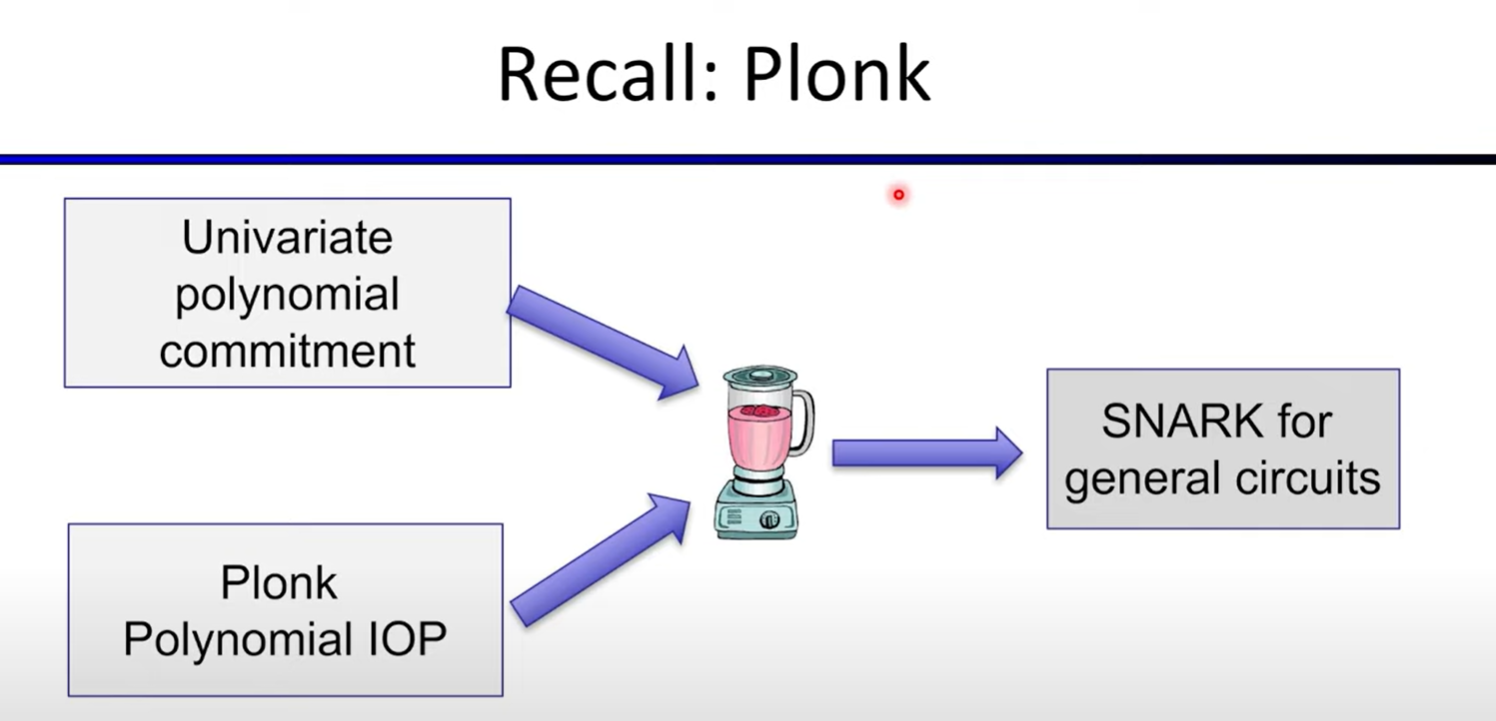
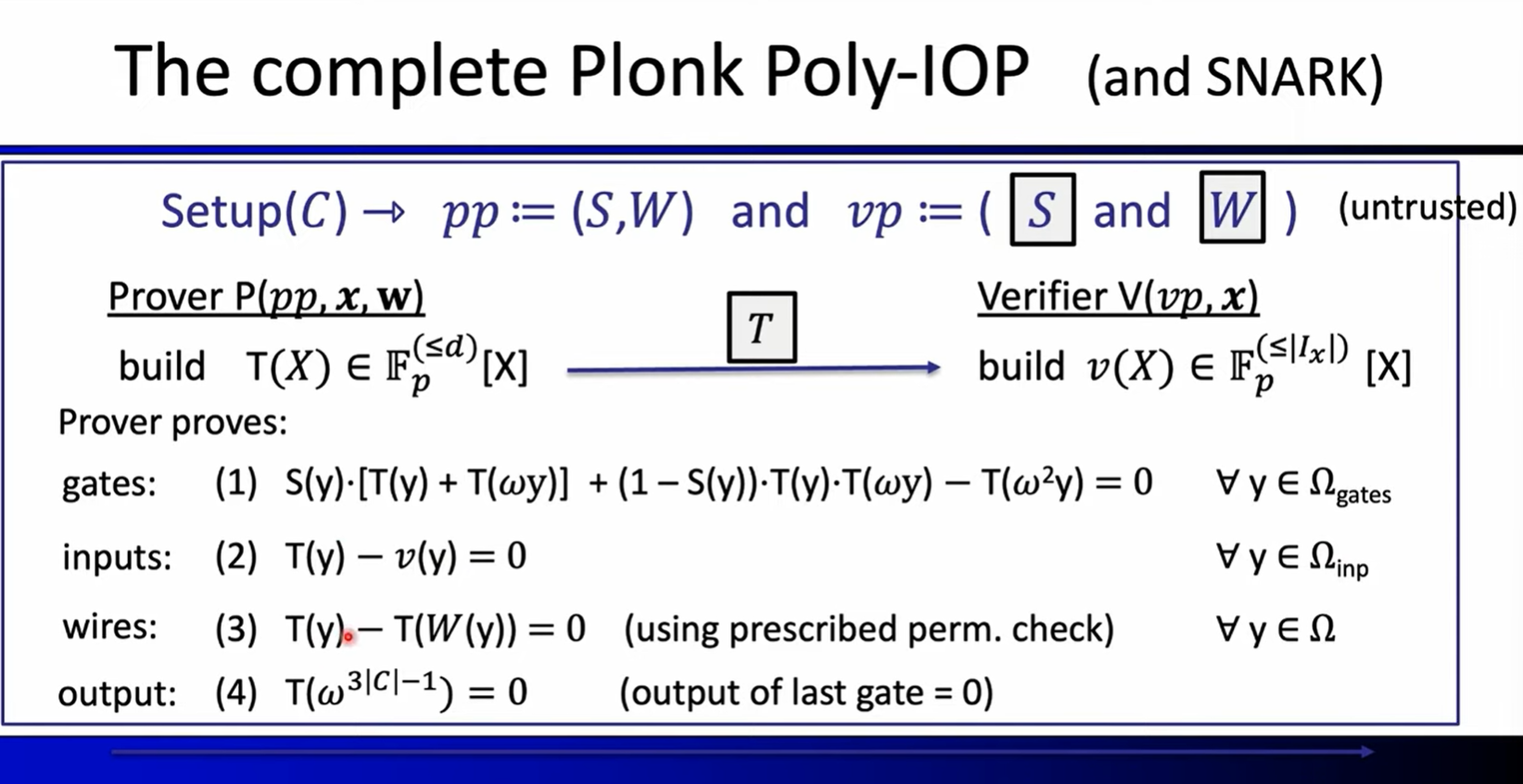
Lecture 5:Plonk SNARK
video: https://www.youtube.com/watch?v=A0oZVEXav24
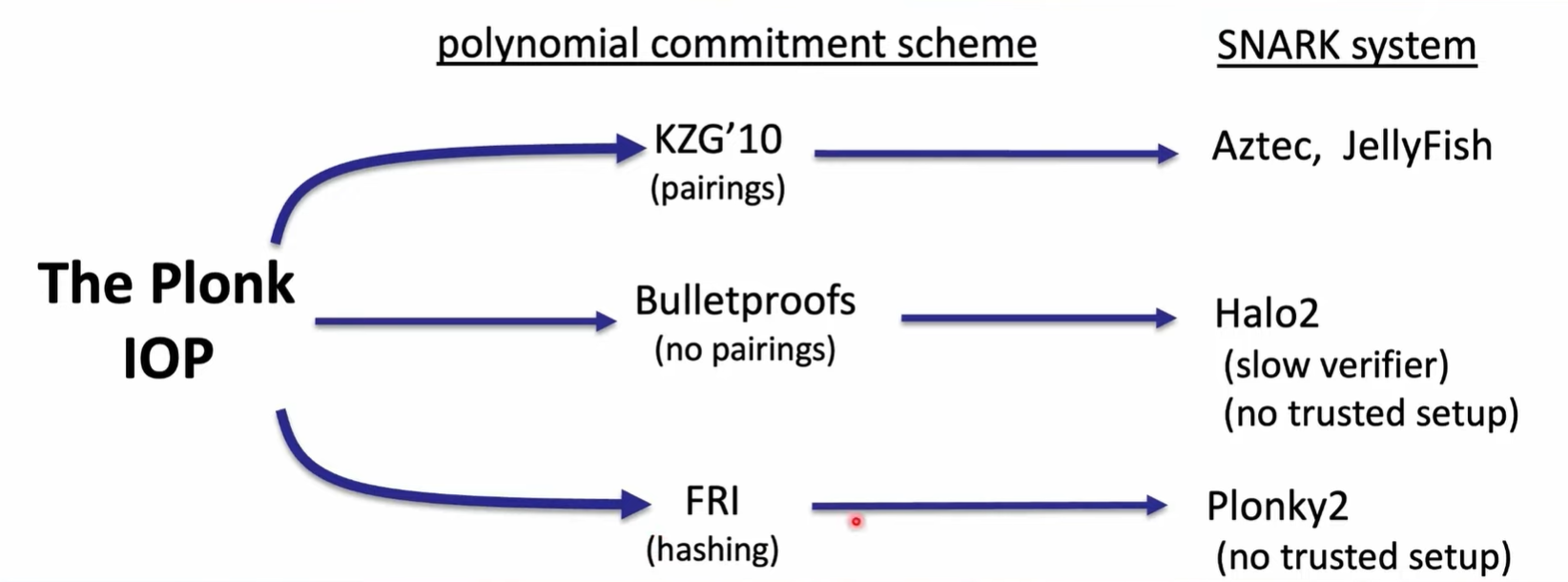

Lecture6: Polynomial Commitments based on Pairing and Discrete Logarithm
video: https://www.youtube.com/watch?v=WyT5KkKBJUw


Background
Group:

Discrete logarithm:

Diffie-Hellman assumption:

Bilinear pairing:

BLS signature:

KZG polynomial commitment






Soundness of KZG:


Knowledge soundness and KoE assumption:


Generic Group model(GGM)

Properties of KZG

Ceremony:

Variants of KZG:
Multivariate poly-commit:

Achieving zero-knowledge:

Batch opening: single polynomial:


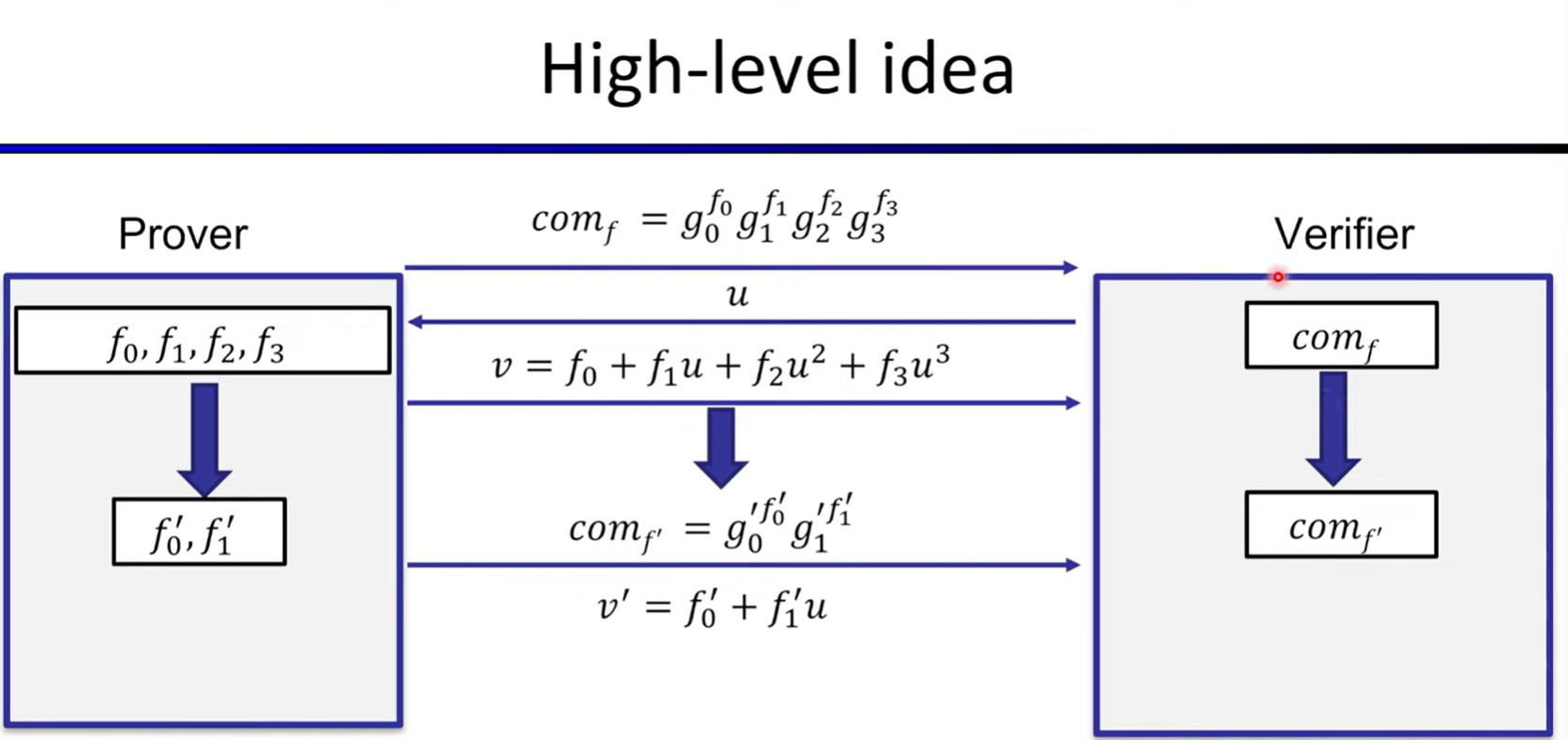
Bulletproofs and other scheme based on discrete-logarithm
Bullteproofs with transparent setup:





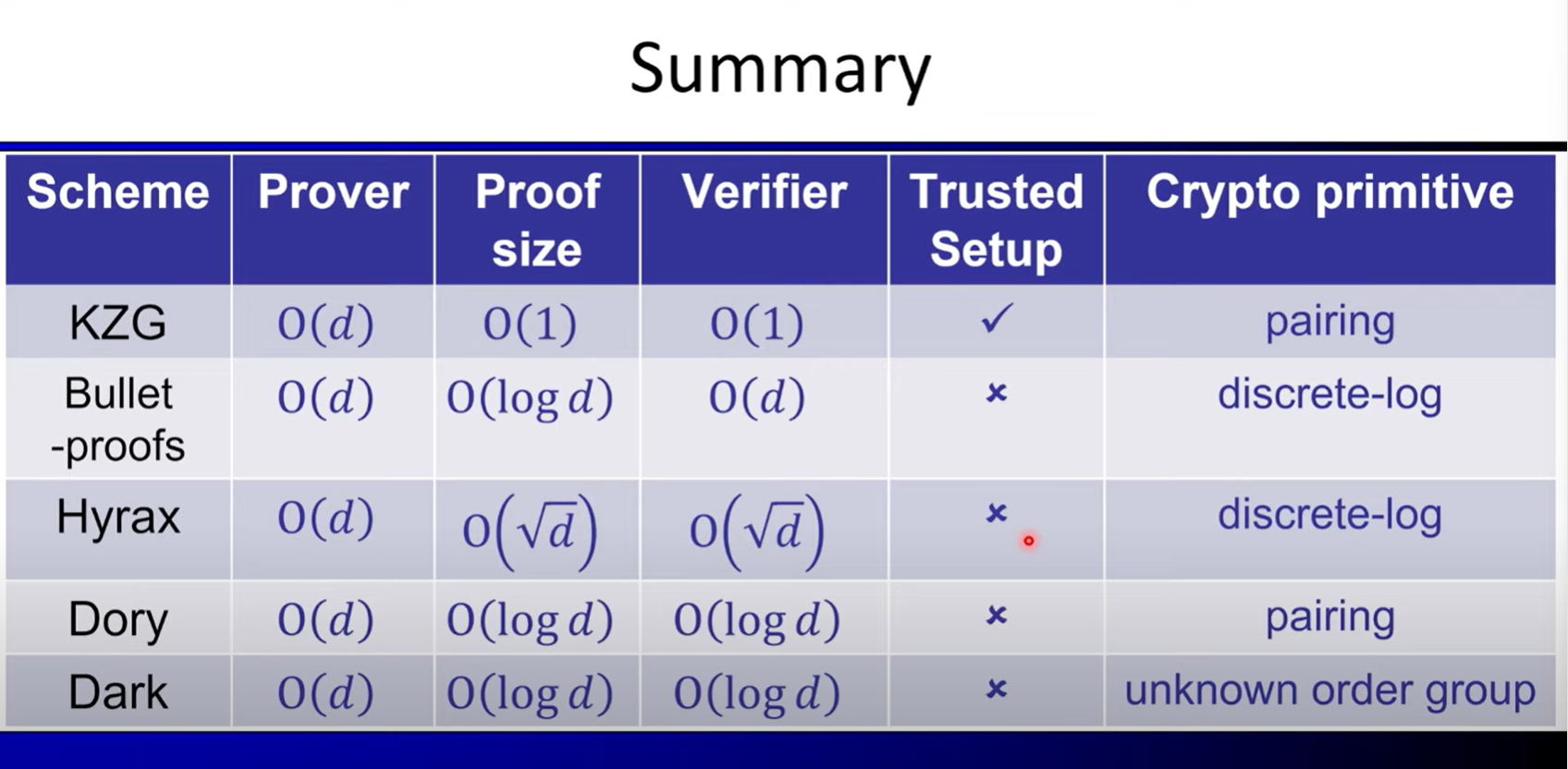
Other polynomial commitment:
Hyrax:

Dory:

Dark:

Lecture7: Polynomial Commitments based on Error-correcting Codes

Background on error-correcting codes
Error-correcting code



Linear code


Polynomial Commitments based on Error-correcting Codes


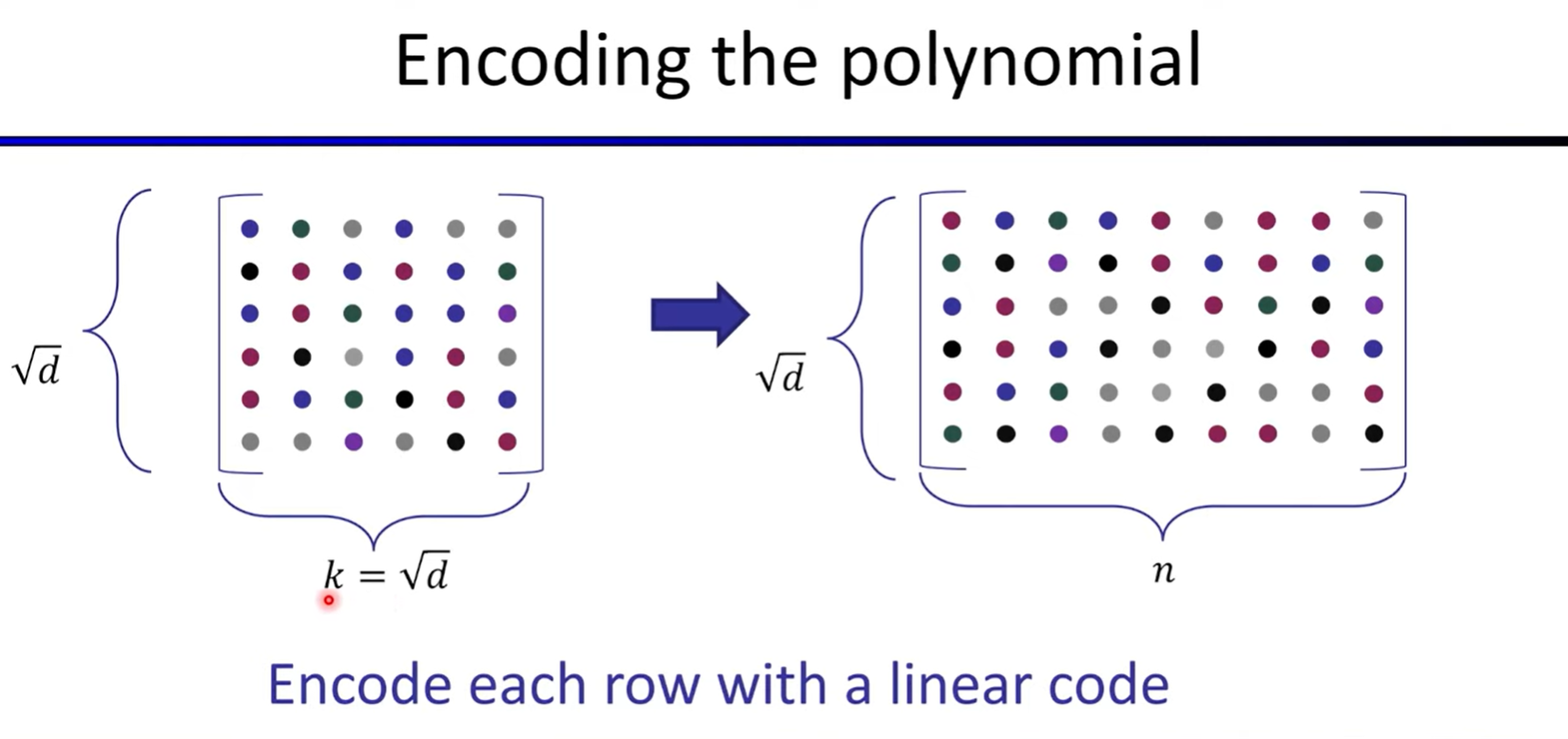
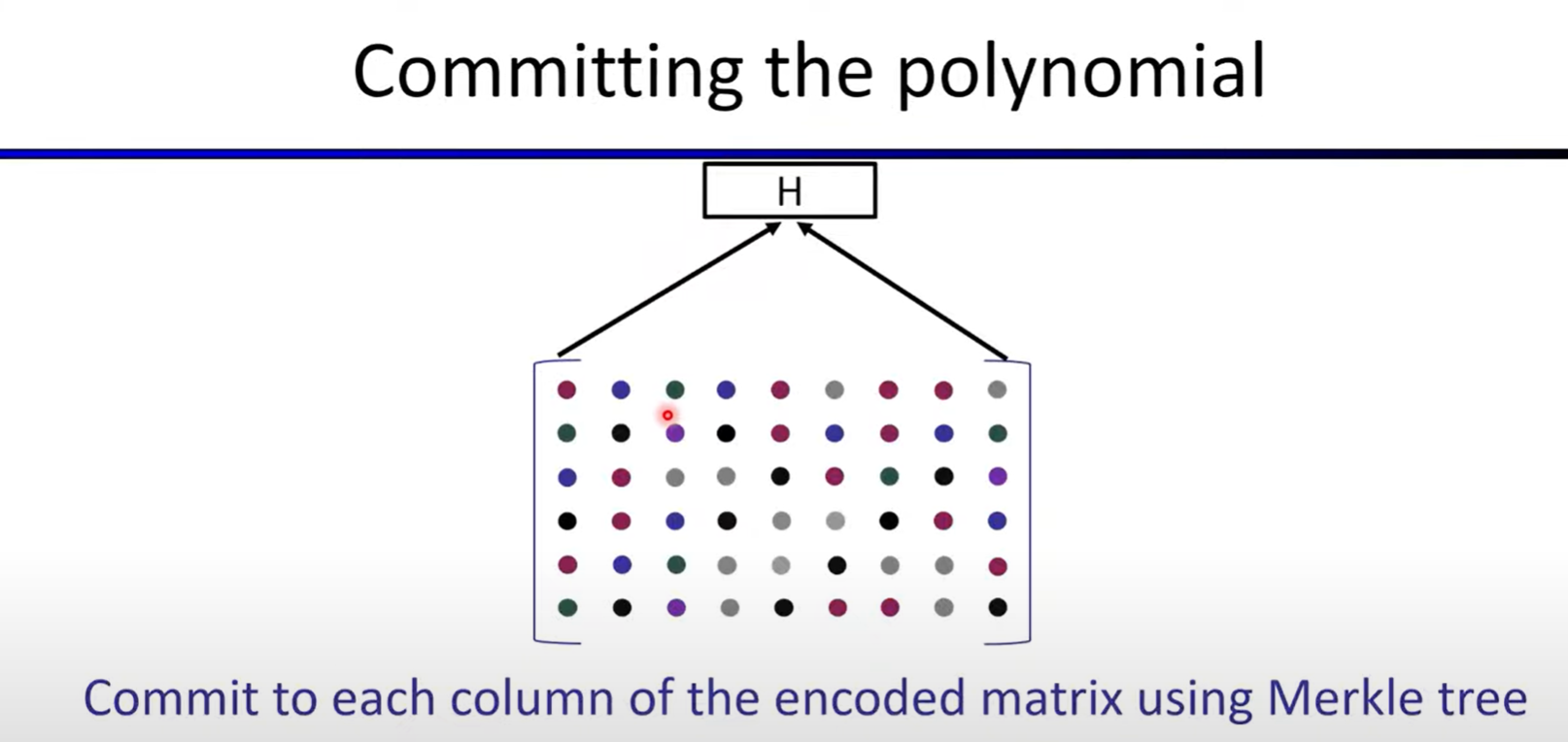

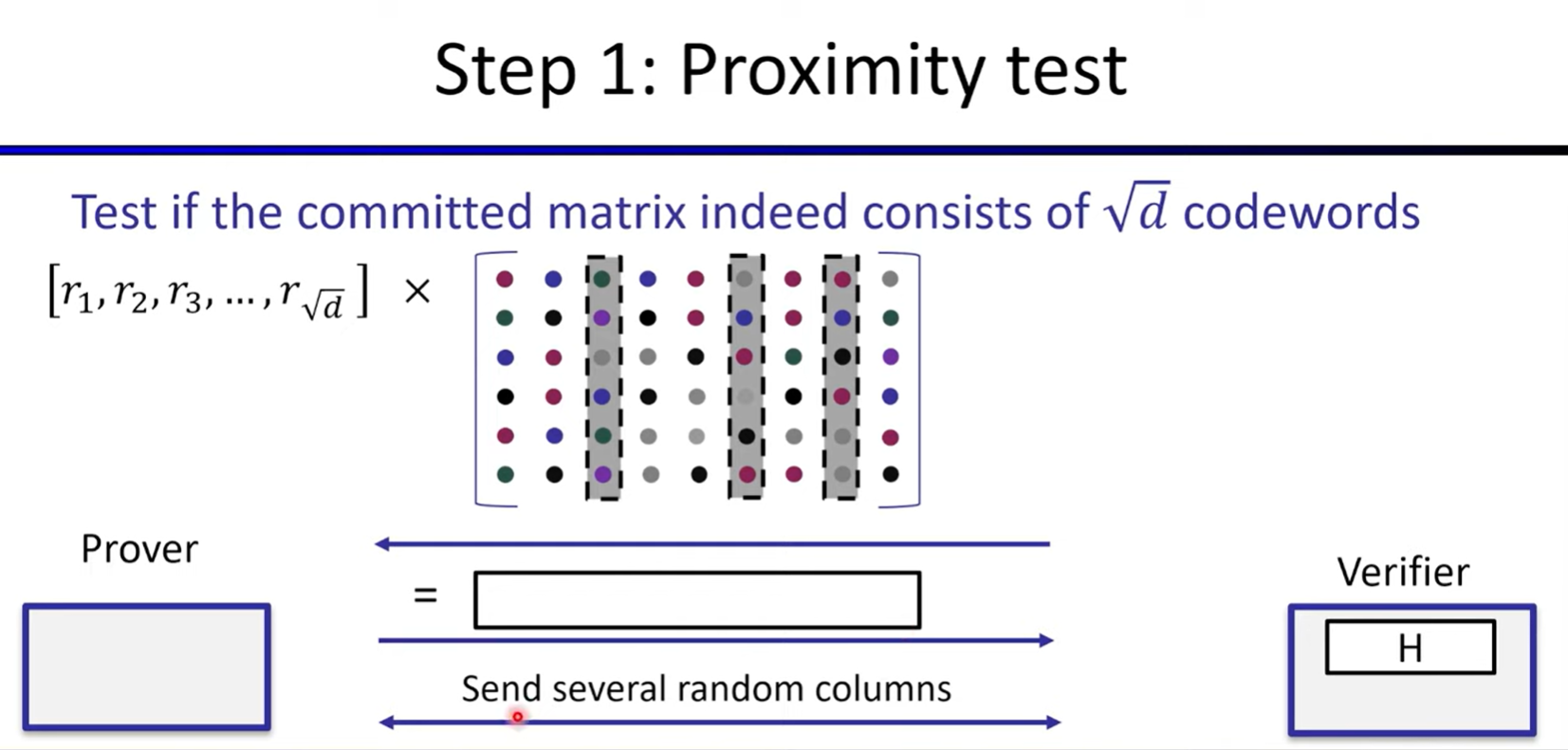
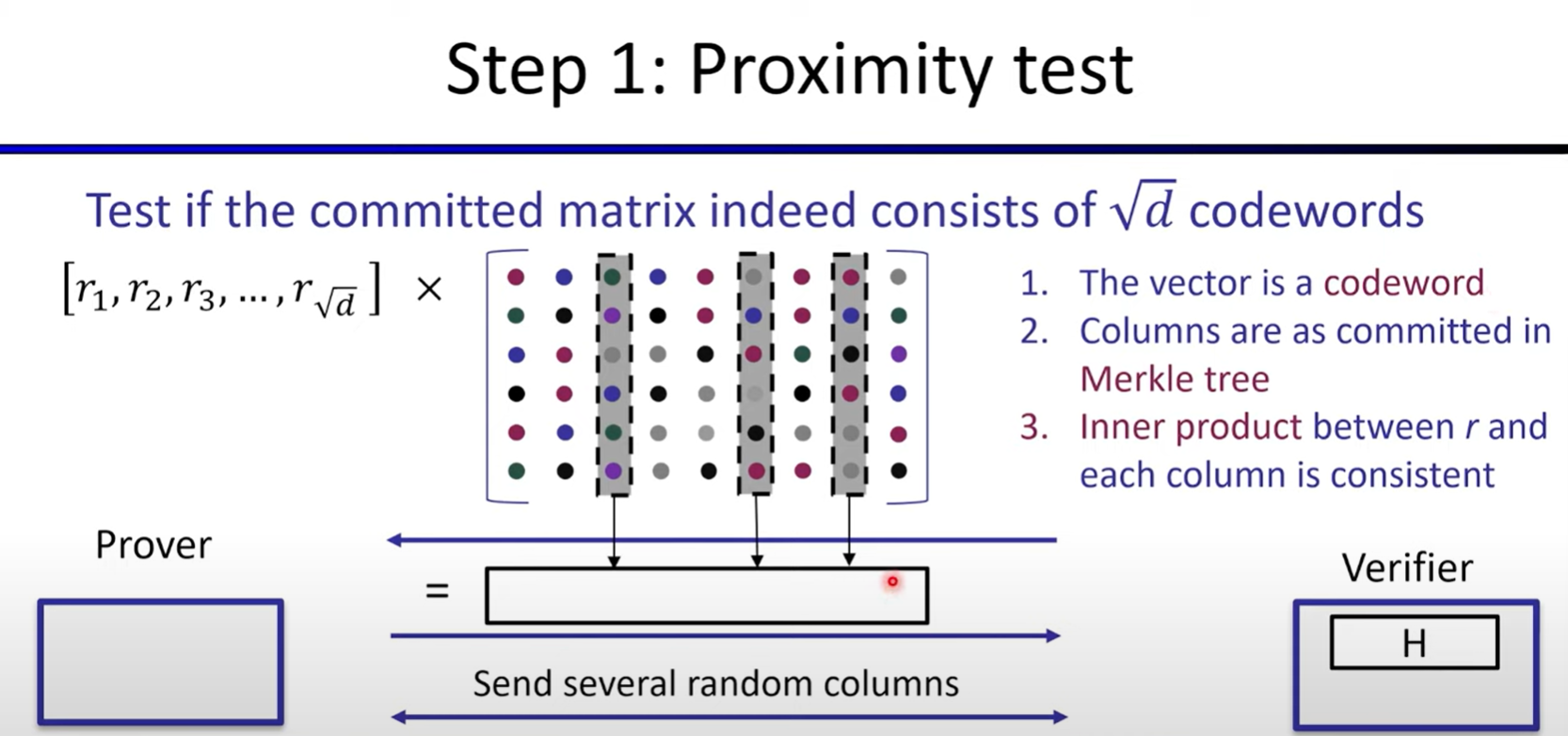
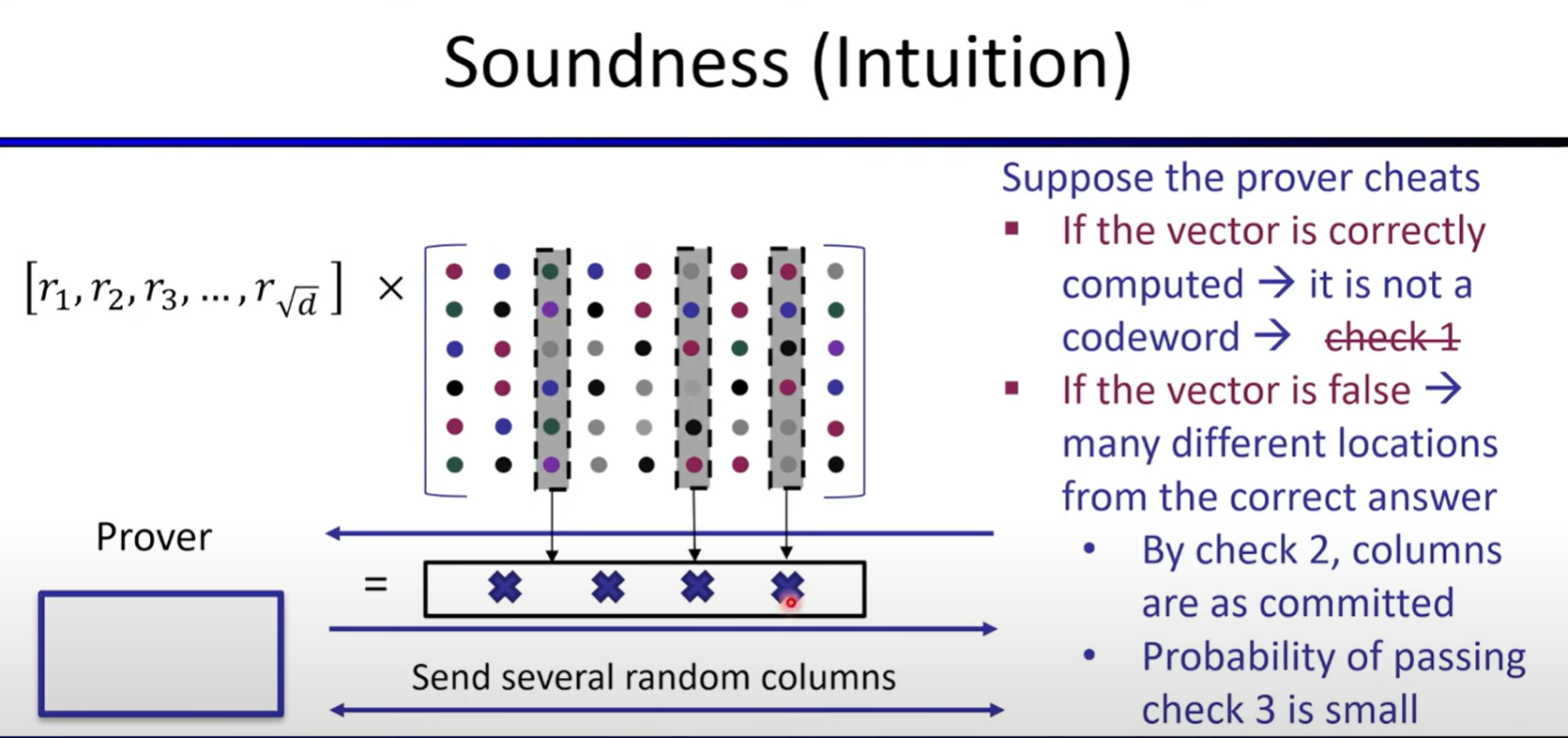


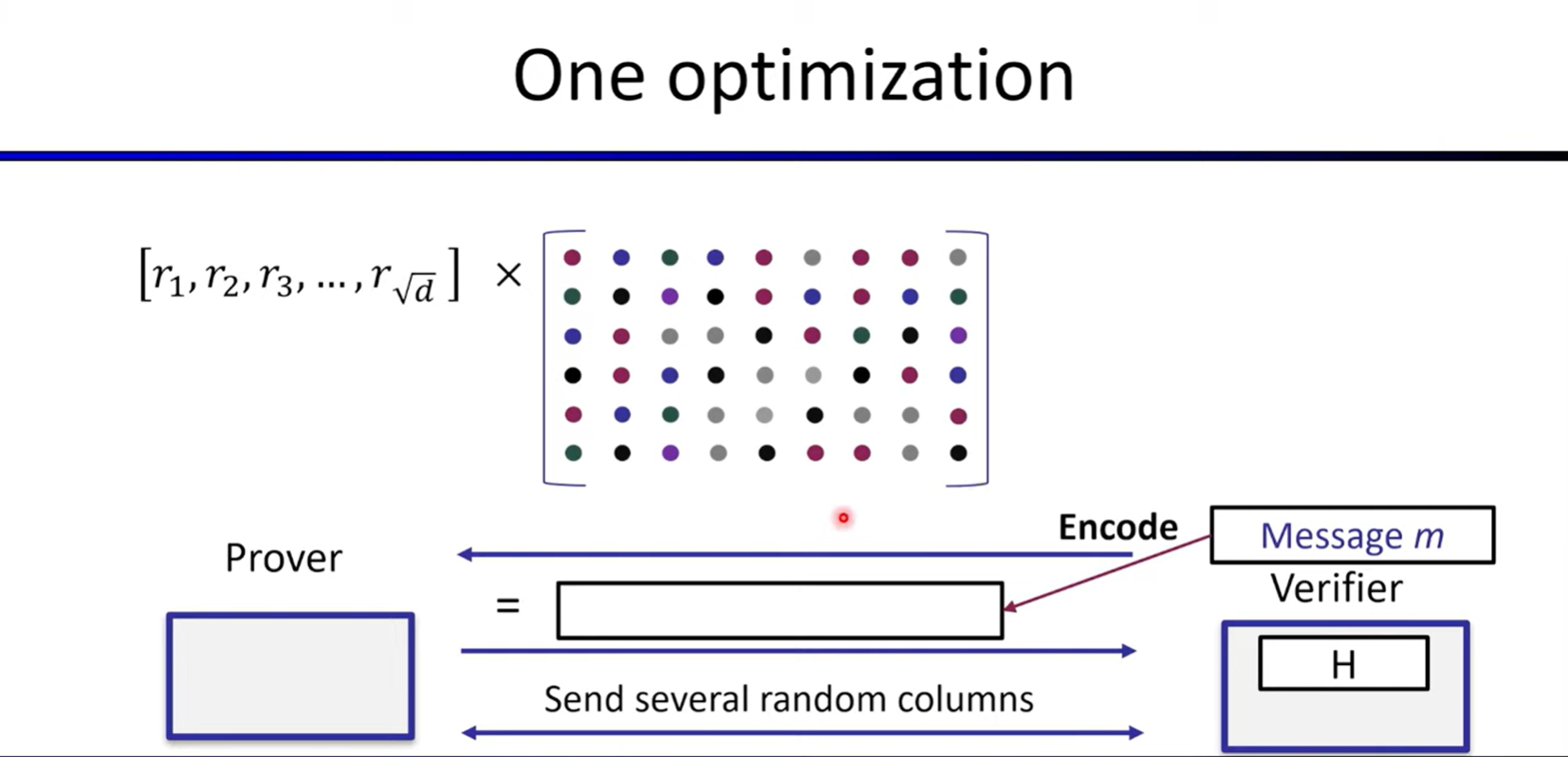
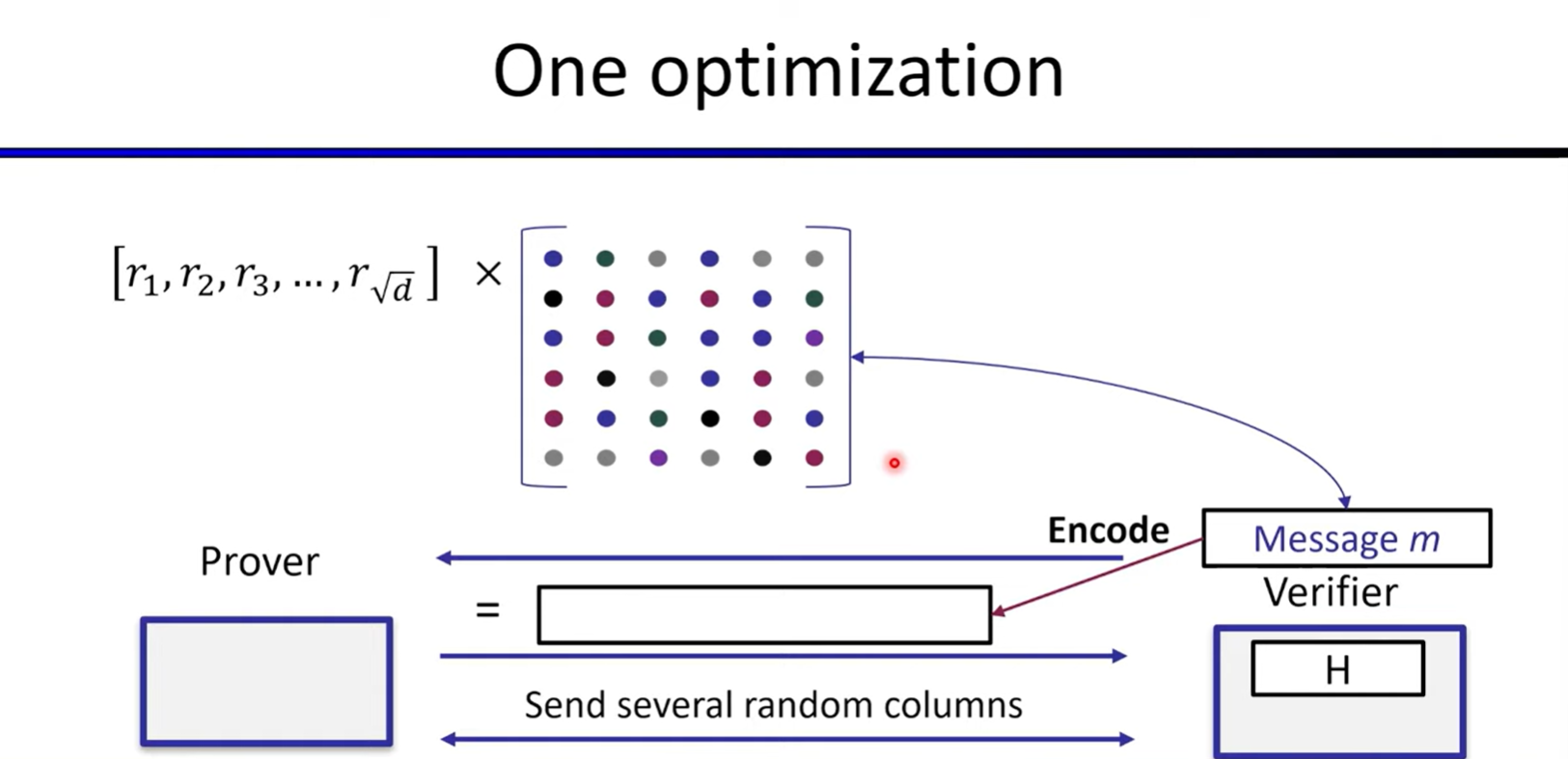
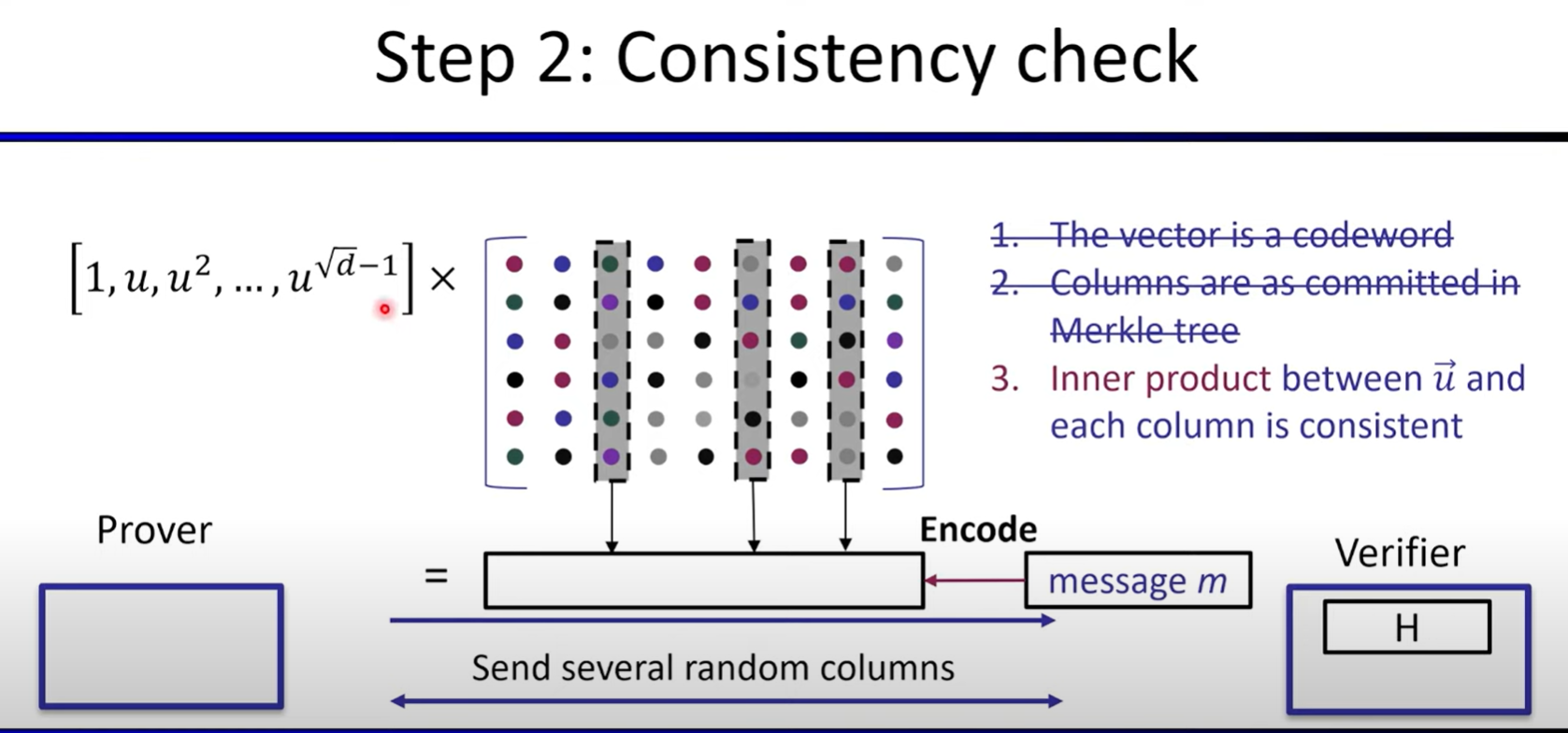





Linear-time encodable code based on expanders
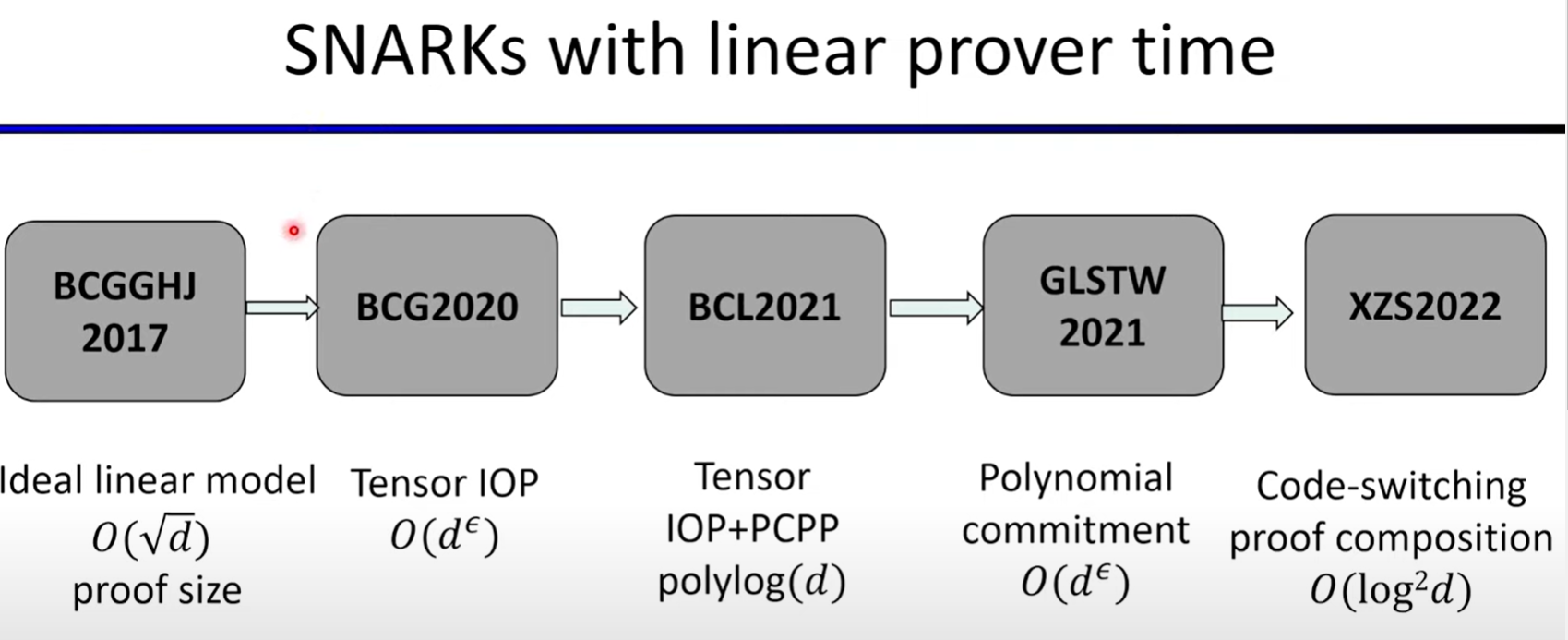
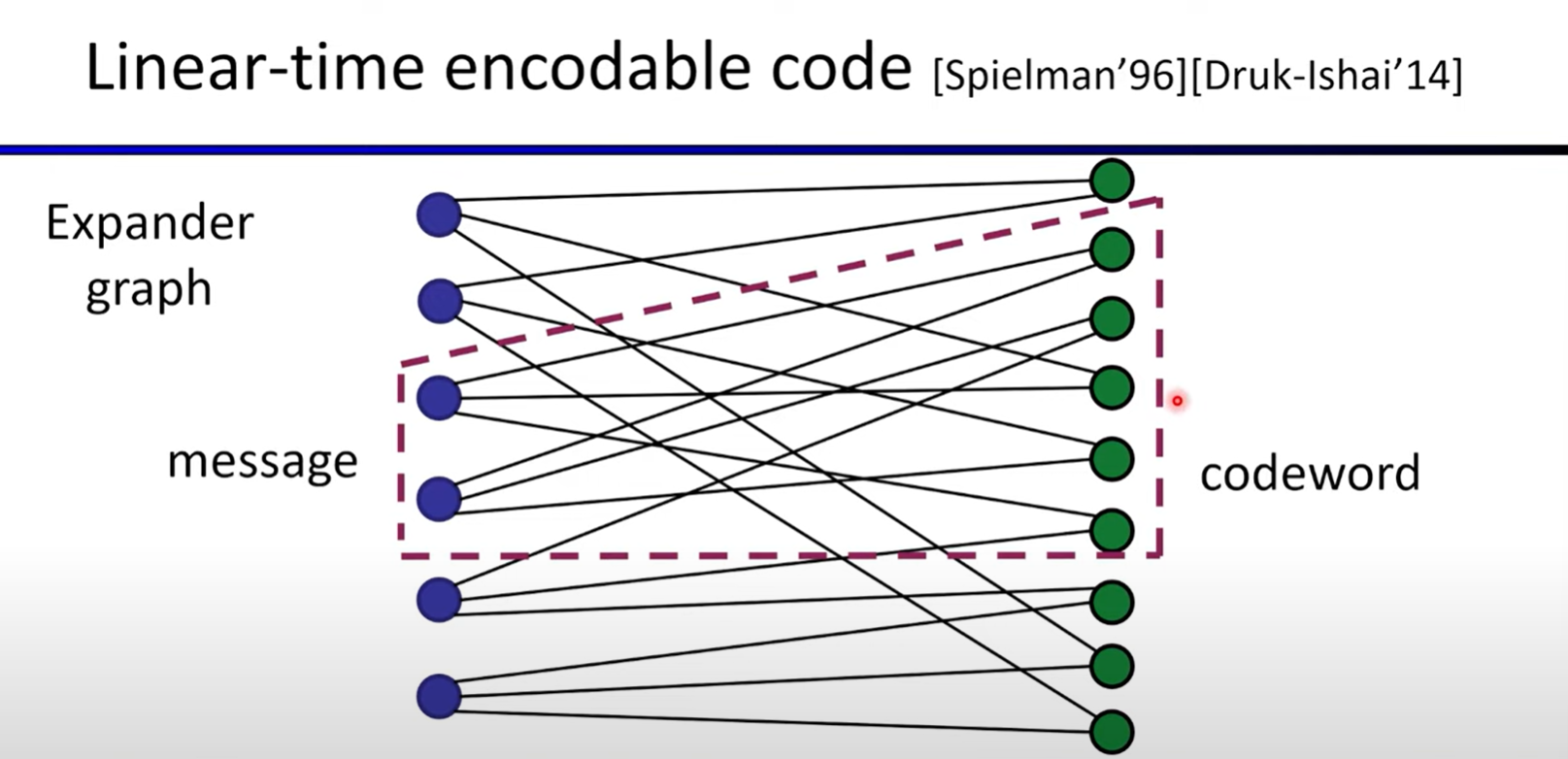
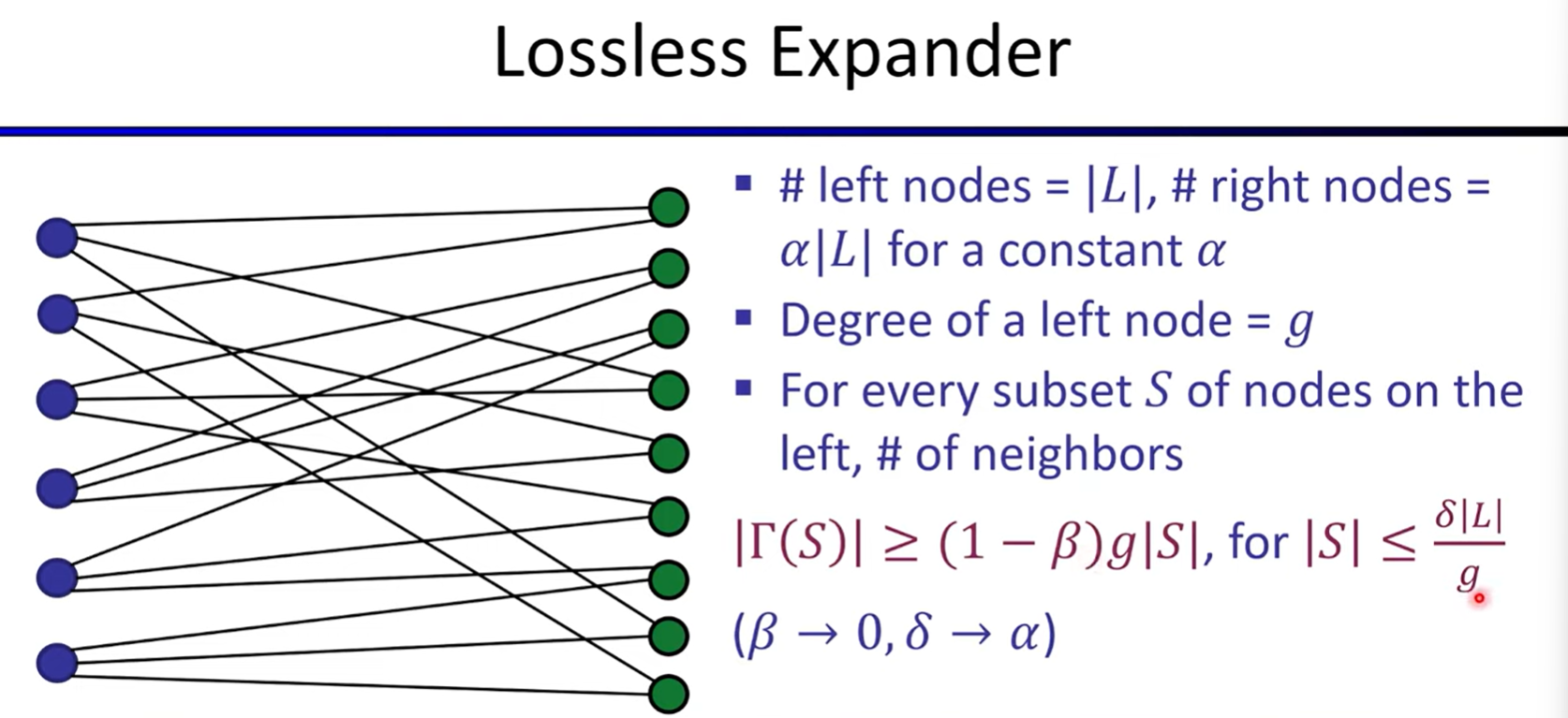
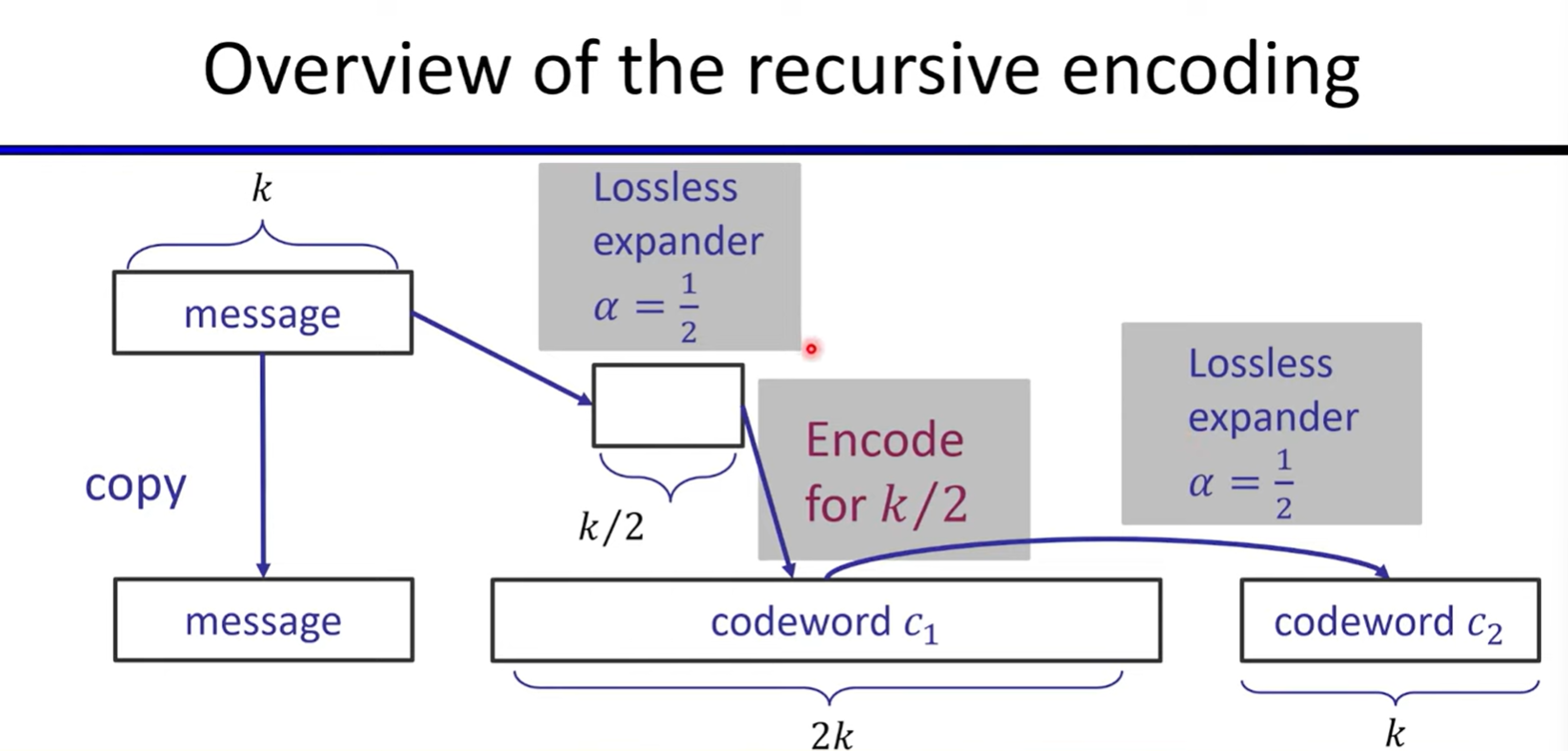


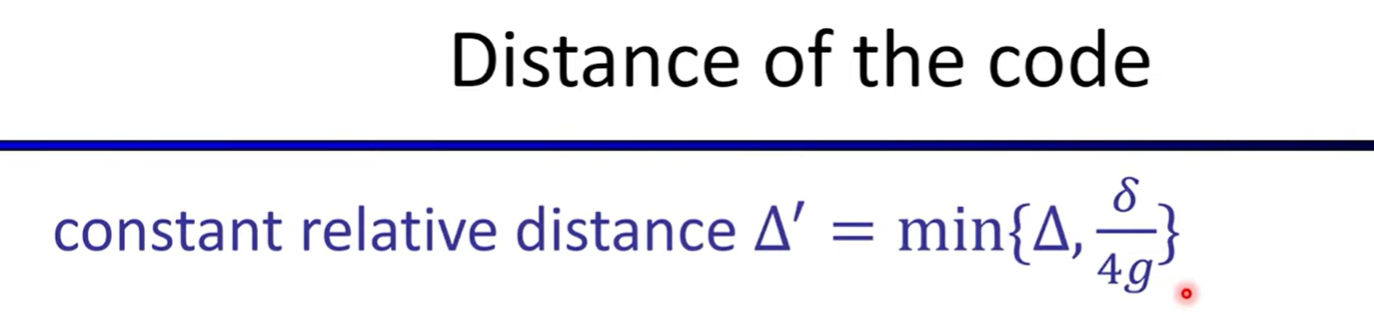



Lecture8: FRI-based Polynomial Commitments and Fiat-Shamir
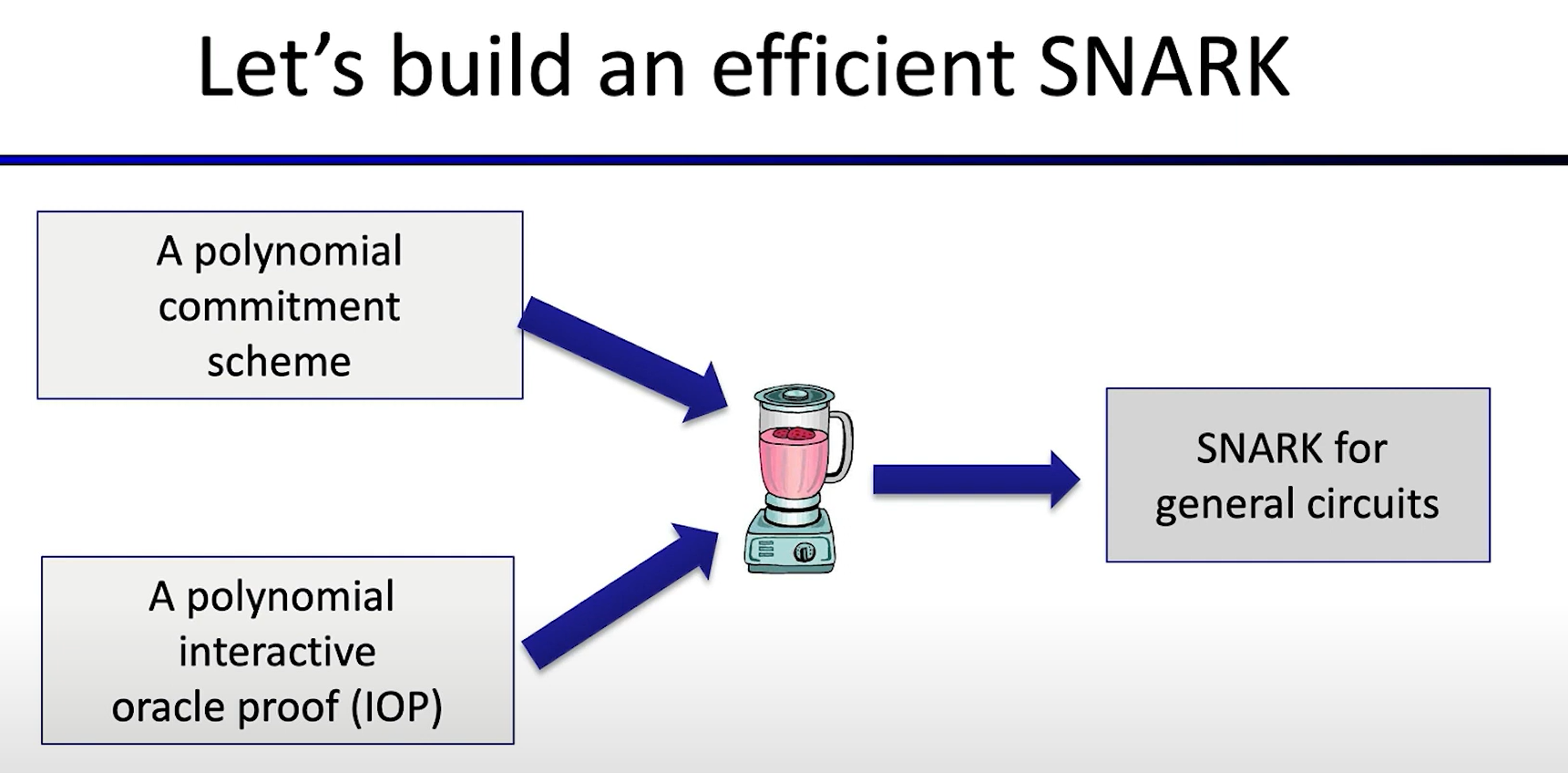
The zoo for Polynomial IOPs and Polynomial commitment


Some specimens from the zoo





FRI(Univariate) Polynomial Commitments


Fix first problem:


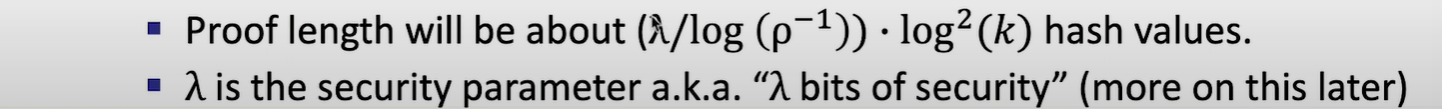

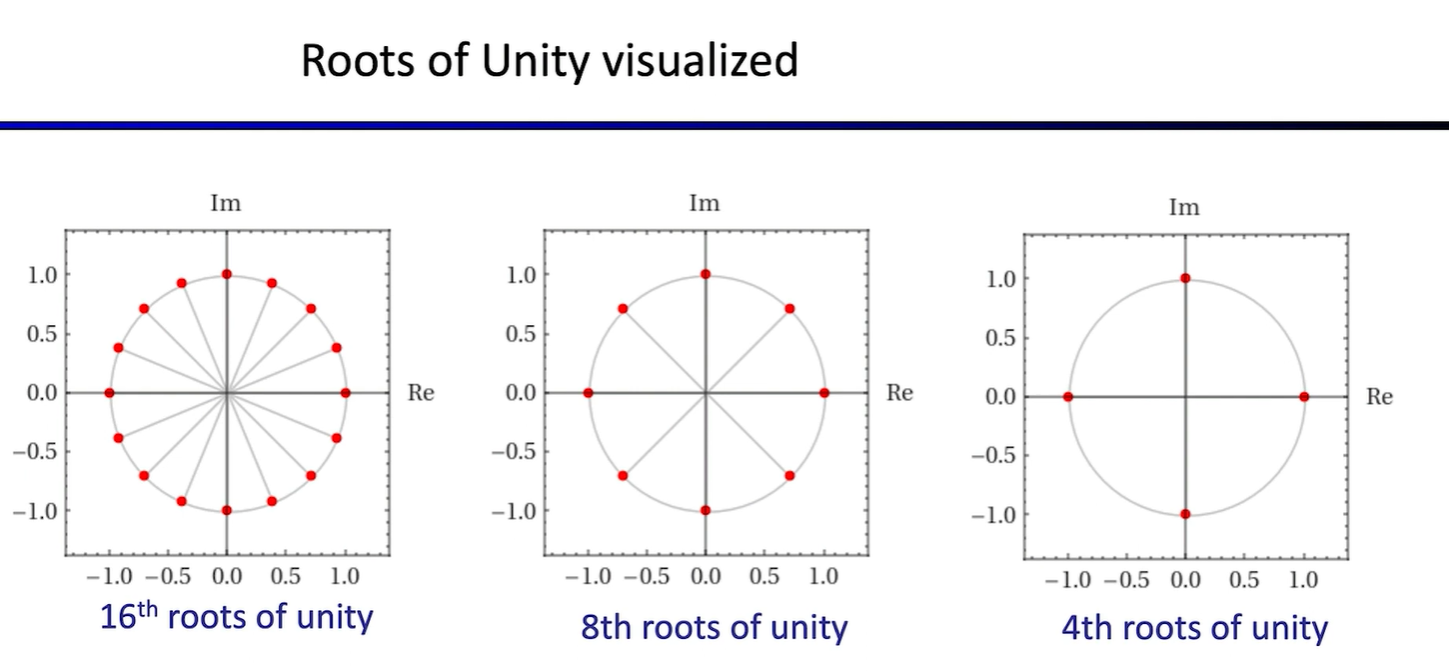


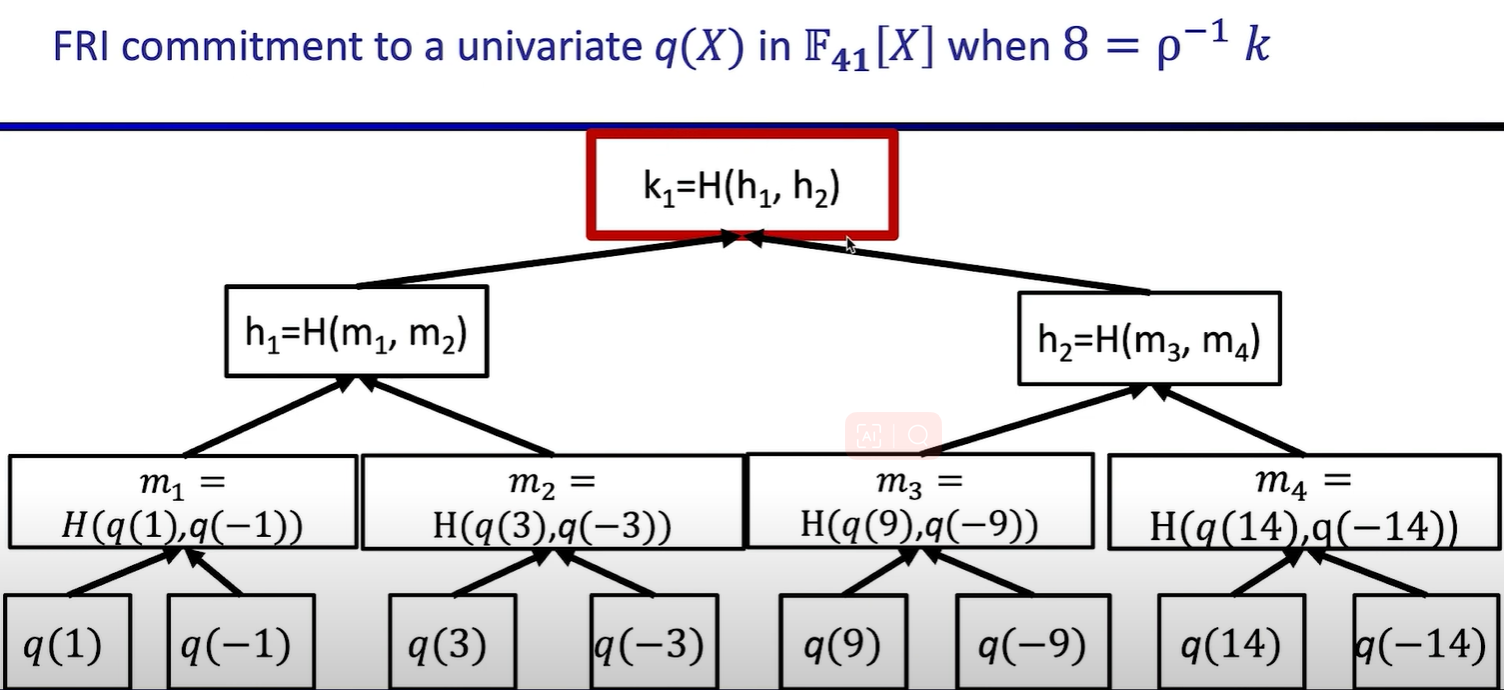
Fix second problem:

文档信息
- 本文作者:Yang Jucai
- 本文链接:https://yangjucai.github.io//2023/06/01/Introduction-to-Zero-Knowledge/
- 版权声明:自由转载-非商用-非衍生-保持署名(创意共享3.0许可证)